【题目】如图,已知正方形ABCD的边长为6厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由点C向点D运动,设运动时间为t秒。
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,EP与PQ有什么关系?请说明理由。
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能使得△EPB与△CQP全等?此时点Q的运动速度为多少?

参考答案:
【答案】(1)EP=PQ,理由见解析;(2)点P,Q运动的时间为![]() 秒,点Q的运动速度为
秒,点Q的运动速度为![]() 厘米/秒.
厘米/秒.
【解析】
(1)根据SAS可判定全等,即可得EP=PQ;
(2)由于点Q的运动速度与点P的运动速度不相等,而运动时间相同,所以BP≠CQ.又△BPE与△CQP全等,则有BP=PC=![]() BC=3厘米,CQ=BE=2厘米,由BP=3厘米求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
BC=3厘米,CQ=BE=2厘米,由BP=3厘米求出运动时间,再根据速度=路程÷时间,即可得出点Q的速度.
(1)EP=PQ,
理由:如图,
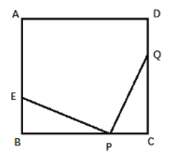
∵点Q的运动速度与点P的运动速度相等,且t=2秒,
∴BP=CQ=2×2=4厘米,
∵AB=BC=6厘米,AE=4厘米,
∴BE=CP=2厘米,
∵四边形ABCD是正方形,
∴在Rt△BPE和Rt△CQP中,
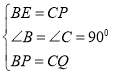 ,
,
∴Rt△BPE≌Rt△CQP,
∴EP=PQ;
(2)∵点Q的运动速度与点P的运动速度不相等,
∴BP≠CQ,
∵∠B=∠C=90°,
∴要使△BPE与△CQP全等,只要BP=PC=3厘米,CQ=BE=2厘米,即可.
∴点P,Q运动的时间t=![]() =
=![]() (秒),
(秒),
此时点Q的运动速度为VQ=![]() =
=![]() =
=![]() (厘米/秒).
(厘米/秒).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:
①若a>0,b>0,则a+b>0;
②若a2=b2,则a=b;
③线段垂直平分线上的点到线段两端点距离相等;
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是( )
A. ①③ B. ②④ C. ③④ D. ②③
-
科目: 来源: 题型:
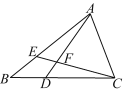
查看答案和解析>>【题目】如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论(1)AD=DF;(2)
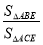 =
=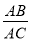 ;(3)
;(3)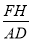 =
=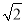 ﹣1;(4)四边形BEHF为菱形.正确的有几个( )
﹣1;(4)四边形BEHF为菱形.正确的有几个( )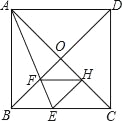
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
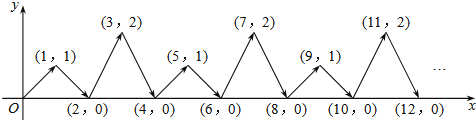
查看答案和解析>>【题目】如图4,动点P在平面直角坐标系中,按图中箭头所示方向运动,第1次从原点运动到点 P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,2),......,按这样的运动规律,经过第2019次运动后,动点P2019的坐标是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育文化用品商店购进篮球和排球共20个,进价和售价如下表,全部销售完后共获利润260元.
篮球
排球
进价(元/个)
80
50
售价(元/个)
95
60
求:(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?
相关试题

