【题目】如图,CA⊥AB,垂足为点A,AB=12,AC=6,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过 秒时,△DEB与△BCA全等.
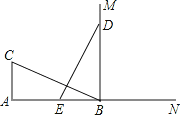
参考答案:
【答案】0,3,9,12.
【解析】
试题分析:此题要分两种情况:①当E在线段AB上时,②当E在BN上,再分别分成两种情况AC=BE,AC=BE进行计算即可.
试题解析:①当E在线段AB上,AC=BE时,△ACB≌△BED,
∵AC=6,
∴BE=6,
∴AE=2-6=6,
∴点E的运动时间为6÷2=3(秒);
②当E在BN上,AC=BE时,
AC=12+6=18,
点E的运动时间为18÷2=9(秒);
③当E在线段AB上,AB=EB时,△ACB≌△BDE,
这时E在A点未动,因此时间为0秒;
④当E在BN上,AB=EB时,△ACB≌△BDE,
AE=12+12=24,
点E的运动时间为24÷2=12(秒),
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=mx-(m-2)过原点,则m的取值范围为( )
A. m>2 B. m<2 C. m=2 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一道题,当a=2,b=﹣2时,求多项式:
3a3b3﹣ a2b+b2﹣3(a3b3﹣
a2b+b2﹣3(a3b3﹣  a2b﹣b2)﹣2b2﹣3的值,马虎做题时把a=2错抄成a=﹣2,王真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.
a2b﹣b2)﹣2b2﹣3的值,马虎做题时把a=2错抄成a=﹣2,王真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,联结AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,将△ABD绕A点逆时针旋转90°,所得到的三角形为 ,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
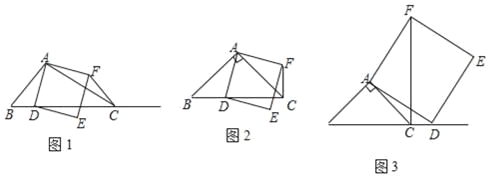
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简x﹣y﹣(x+y)的最后结果是( )
A.0
B.2x
C.﹣2y
D.2x﹣2y -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个数的绝对值相等,那么这两个数_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学库存若干套桌椅,准备修理.现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修理桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元的修理费.
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a,由甲单独修理;b,由乙单独修理;c,甲、乙合作同时修理.你认为哪种方案省时又省钱?为什么?
相关试题

