【题目】随着“一带一路”的不断建设与深化,我国不少知名企业都积极拓展海外市场,参与投资经营.某著名手机公司在某国经销某种型号的手机,受该国政府经济政策与国民购买力双重影响,手机价格不断下降.分公司在该国某城市的一家手机销售门店,今年5月份的手机售价比去年同期每台降价1000元,若卖出同样多的手机,去年销售额可达10万元,今年销售额只有8万元.
(1)今年5月份每台手机售价多少元?
(2)为增加收入,分公司决定拓展产品线,增加经销某种新型笔记本电脑.已知手机每台成本为3500元,笔记本电脑每台成本为3000元,分公司预计用不少于4.8万元的成本资金少量试生产这两种产品共15台,但因资金所限不能超过5万元,共有几种生产方案?
(3)如果笔记本电脑每台售价3800元,现为打开笔记本电脑的销路,公司决定每售出1台笔记本电脑,就返还顾客现金a元,要使(2)中各方案获利最大,a的值应为多少?最大利润多少?
参考答案:
【答案】(1)今年5月份每台手机售价4000元;(2)5种生产方案;(3)a的值应为300元,最大利润为7500元.
【解析】
(1)设今年5月份手机每台售价为m元,则去年同期每台售价为(m+1000)元,根据数量=总价÷单价结合今年5月份与去年同期的销售数量相同,即可得出关于m的分式方程,解之经检验后即可得出结论;
(2)设生产手机x台,则生产笔记本电脑(15-x)台,根据总价=单价×数量结合总价不少于4.8万元不能超过高于5万元,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,由该范围内整数的个数即可得出方案的种数;
(3)设总获利为w元,根据利润=销售收入-成本,即可得出w关于x的一次函数关系式,由w的值与x无关,即可得出a-300=0,解之即可求出a值.
(1)设今年5月份手机每台售价为m元,则去年同期每台售价为(m+1000)元,
根据题意得:![]() ,
,
解得:m=4000,
经检验,m=4000是原方程的根且符合题意.
答:今年5月份手机每台售价为4000元.
(2)设生产手机x台,则生产笔记本电脑(15-x)台,
根据题意得: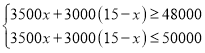 ,
,
解得:6≤x≤10,
∴x的正整数解为6、7、8、9、10.
答:共有5种生产方案.
(3)设总获利为w元,
根据题意得:w=(4000-3500)x+(3800-3000-a)(15-x)=(a-300)x+12000-15a.
∵w的值与x值无关,
∴a-300=0,即a=300.
当a=300时,最大利润为12000-15×300=7500元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张师傅在铺瓷砖时发现,用8块大小一样的小长方形瓷砖恰好可以拼成一个大的长方形,如图①.然后,他用这8块瓷砖又拼出一个正方形,如图②,中间恰好空出一个边长为1的小正方形(阴影部分).
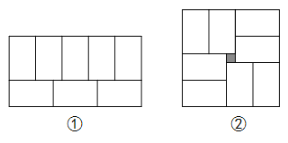
(1)请你根据图①写出小长方形的长与宽之比为 ;
(2)请你根据图②列出方程,求出小长方形的长与宽.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).

(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果批发商欲将A市的一批水果运往B市销售,有火车和汽车两种运输工具,运输过程中的损耗均为160元/时。有关数据如下:
运输工具
平均速度(千米/时)
运费(元/千米)
装卸费(元)
火车
100
18
1800
汽车
80
22
1000
(1)如果汽车的总支出费用比火车费用多960元,求出A市与B市之间的路程是多少千米?请列方程解答。
(2)如果A市与C市之间的距离为300千米,要想将这批水果运往C市销售。选择哪种运输工具比较合算呢?请通过计算说明你的理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=-
 x+b的图象与反比例函数y2=
x+b的图象与反比例函数y2= (x>0)的图象交于A、B两点,与x轴交于点C,且点A的坐标为(1,2),点B的横坐标为3.
(x>0)的图象交于A、B两点,与x轴交于点C,且点A的坐标为(1,2),点B的横坐标为3.(1)在第一象限内,当x取何值时,y1>y2?(根据图直接写出结果)
(2)求反比例函数的解析式及△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸片ABCD沿对角线BD折叠,点C的对应点为C′,再将所折得的图形沿EF折叠,使得点D和点A重合.若AB=3,BC=4,则折痕EF的长为__________.
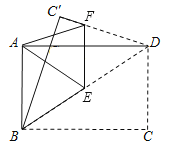
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.

相关试题

