【题目】已知等边![]() 的边长为2,现将等边
的边长为2,现将等边![]() 放置在平面直角坐标系中,点B和原点重合,点C在x轴正方向上,直线交x轴于点D,交y轴于点E,且
放置在平面直角坐标系中,点B和原点重合,点C在x轴正方向上,直线交x轴于点D,交y轴于点E,且![]() 如图
如图![]() ,现将等边
,现将等边![]() 从图1的位置沿x轴正方向以每秒1个单位长度的速度移动,边AB、AC分别与线段DE交于点G、
从图1的位置沿x轴正方向以每秒1个单位长度的速度移动,边AB、AC分别与线段DE交于点G、![]() 如图
如图![]() ,同时点P从
,同时点P从![]() 的顶点B出发,以每秒2个单位长度的速度沿折线
的顶点B出发,以每秒2个单位长度的速度沿折线![]() 运动
运动![]() 当点P运动到C时即停止活动,
当点P运动到C时即停止活动,![]() 也随之停止移动,设
也随之停止移动,设![]() 平移的时间为
平移的时间为![]() .
.
![]() 试求直线DE的解析式;
试求直线DE的解析式;
![]() 当点P在线段AC上运动时,设点P与点H的距离为y,求y与t的函数关系式,并写出定义域;
当点P在线段AC上运动时,设点P与点H的距离为y,求y与t的函数关系式,并写出定义域;
![]() 当点P在线段AB上运动时,
当点P在线段AB上运动时,![]() 中恰好有一个角的度数为
中恰好有一个角的度数为![]() ,请直接写出t的值,不必写过程.
,请直接写出t的值,不必写过程.

参考答案:
【答案】![]() 当运动时间t为
当运动时间t为![]() 秒或
秒或![]() 秒或1秒时,
秒或1秒时,![]() 中恰好有一个角的度数为
中恰好有一个角的度数为![]()
【解析】
![]() 根据等边三角形的性质结合
根据等边三角形的性质结合![]() ,可得出
,可得出![]() ,结合AB的长度可得出OE、OD的长度,进而可得出点D、E的坐标,利用待定系数法即可求出直线DE的解析式;
,结合AB的长度可得出OE、OD的长度,进而可得出点D、E的坐标,利用待定系数法即可求出直线DE的解析式;
![]() 根据点P、C的运动速度可得出PA、CD的值,由
根据点P、C的运动速度可得出PA、CD的值,由![]() 、
、![]() 可得出
可得出![]() ,进而可得出CH的长,再根据
,进而可得出CH的长,再根据![]() 即可找出y与t的函数关系式;
即可找出y与t的函数关系式;
![]() 分点P、A重合及点P、A不重合两种情况考虑:
分点P、A重合及点P、A不重合两种情况考虑:![]() 当点P、A重合时,即
当点P、A重合时,即![]() 时,符合题意,由
时,符合题意,由![]() 可求出t值;
可求出t值;![]() 当点P、A不重合时,分
当点P、A不重合时,分![]() 和
和![]() 两种情况考虑,通过解直角三角形即可求出t值
两种情况考虑,通过解直角三角形即可求出t值![]() 综上即可得出结论.
综上即可得出结论.
解:![]() 为等边三角形,
为等边三角形,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 点D的坐标为
点D的坐标为![]() ,点E的坐标为
,点E的坐标为![]()
设直线DE的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,得:
,得:
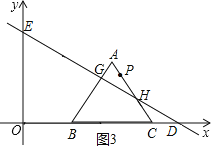
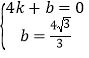 ,解得:
,解得: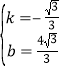 ,
,
![]() 直线DE的解析式为
直线DE的解析式为![]() .
.
![]() 如图3,
如图3,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 点P在AC上,
点P在AC上,
![]() ,
,
![]() .
.
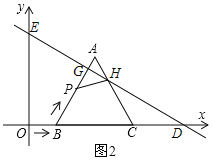
![]() 如图2,
如图2,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() 当点P、A重合时,即
当点P、A重合时,即![]() 时,符合题意,
时,符合题意,
此时![]() ;
;
![]() 当点P、A不重合时,
当点P、A不重合时,![]() ,
,![]() ,
,![]()
若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() .
.
综上所述:当运动时间t为![]() 秒或
秒或![]() 秒或1秒时,
秒或1秒时,![]() 中恰好有一个角的度数为
中恰好有一个角的度数为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )

A.8
B.10
C.12
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )

A.50°
B.51°
C.51.5°
D.52.5° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )

A.π
B.π+5
C.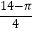
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
提供的三个条件是:①AB=DE;②AC=DF;③AC∥DF.

相关试题

