Question

【题目】如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为(0，2)，D为⊙C在第一象限内的一点，且∠ODB＝60°.

(1)求⊙C的半径；

(2)求圆心C的坐标．

Answer 1

【答案】（1）2（2）（，1）

【解析】试题分析：⑴ 根据同弧所对的圆周角度数相等可得∠AOB的度数，然后根据特殊角三角函数值可得直径AB的长，进而求得圆的半径长度.

(2)先利用勾股定理求出OB的长，再利用垂径定理求得OE、OF的长度，即可得到点C的坐标.

试题解析：⑴ 连接AB，如图所示，

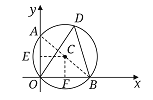
∵∠ AOB＝90°，∴ AB是⊙ C的直径．

∵∠ ODB＝60°，∴ ∠ OAB＝60°.

∵点A的坐标为(0，2)，∴ OA＝2.

在Rt△ AOB中，∠ OAB＝60°，∴ AB＝2OA＝4，∴ ⊙ C的半径为2.

(2)如上图所示，过点C坐CE⊥OA与点E，CF⊥OB与点F，则Rt△AOB中，由勾股定理可得， ，由垂径定理可知， ，

，又因为点C在第一象限，故圆心C的坐标为（ ，1）.