【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与圆O交于点E,连结BE、DE.
(1)若圆的半径是3,∠EBA是30度,求AD的长度.
(2)求证:∠BED=∠C.
(3)若OA=5,AD=8,求切线AC的长.
参考答案:
【答案】
(1)解:∵∠EBA是30度,
∴∠AOF=60°,
∵OC⊥AD,
∴∠OAF=30°,AD=2AF,
∵AO=3,
∴AF= ![]() ,
,
∴AD=2AF=3 ![]()
(2)解:∵AC是⊙O的切线,AB是⊙O直径,
∴AB⊥AC.
则∠1+∠2=90°,
又∵OC⊥AD,
∴∠1+∠C=90°,
∴∠C=∠2,
而∠BED=∠2,
∴∠BED=∠C
(3)解:连接BD,

∵AB是⊙O直径,
∴∠ADB=90°,
∴BD= ![]() =
= ![]() =6,
=6,
∴△OAC∽△BDA,
∴OA:BD=AC:DA,
即5:6=AC:8,
∴AC= ![]()
【解析】(1)利用垂径定理和圆周角定理,先求AF再求AD;(2)可连BD,构成直径所对的90度圆周角,再利用圆周角定理可转化∠C=∠2,∠BED=∠2,得出结论;(3)可证△OAC∽△BDA,利用对应边成比例求出AC.
【考点精析】通过灵活运用切线的性质定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P以2cm/s的速度沿如图所示的边框从B-C-D-E-F-A的路径运动,记△ABP的面积为S (cm2), S与运动时间t (s)的关系如图所示,若AB=6cm,请回答下列问题:
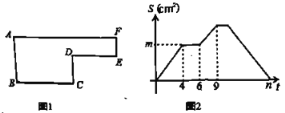
(1)如图中BC=______cm, CD=______cm,DE=______cm
(2)求出如图中边框所围成图形的面积;
(3)求如图中m、n的值;
(4)分别求出当点P在线段BC和DE上运动时S与t的关系式,并写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为
A. 3.7×10﹣5克 B. 3.7×10﹣6克 C. 37×10﹣7克 D. 3.7×10﹣8克
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=∠CBA,过点A向右作AD∥BC,点E是射线AD上的一个动点,∠ACE的平分线交BA的延长线于点F.
(1)若∠ACB=40°,∠ACE=38°,求∠F的度数;
(2)在动点E运动的过程中,
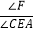 的值是否发生变化?若不变,求它的值;若变化,请说明理由.
的值是否发生变化?若不变,求它的值;若变化,请说明理由.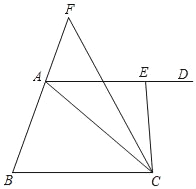
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过平移,△ABC移到△DEF的位置,如图,下列结论:①AD=BE=CF,且AD∥BE∥CF;②AB∥DE,BC∥EF,BC=EF;③AB=DE,BC=EF,AC=DF.正确的有( )
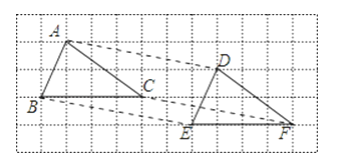
A. 0B. 1C. 2D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别次数x频数和(人数)
第1组80≤x<1006
第2组100≤x<1208
第3组120≤x<140a
第4组140≤x<16018
第5组160≤x<1806.
请结合图表完成下列问题:
(1)表中的a=;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140,为合格;140≤x<160为良;x≥160为优.根据以上信息,请你给学校或九年级同学提一条合理化建议: . -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年9月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元。 甲种商品与乙种商品的销售单价各多少元?
相关试题

