【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
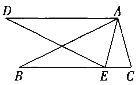
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
参考答案:
【答案】(1)、证明过程见解析;(2)、30°
【解析】
试题分析:(1)、根据∠BAC=∠DAE,AB=AD,∠B=∠D得出三角形全等;(2)、根据全等得出∠CAE的旋转角,然后根据等腰三角形的性质得出∠ACE=∠AEC=75°,最后根据三角形的内角和定理求出旋转角度.
试题解析:(1)、∵∠BAC=∠DAE,AB=AD,∠B=∠D,∴△ABD≌△ADE.
(2)、∵△ABC≌△ADE, ∴AC与AE是一组对应边, ∴∠CAE的旋转角,
∵AE=AC,∠AEC=75°, ∴∠ACE=∠AEC=75°, ∴∠CAE=180°—75°—75°=30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的一组是( )
A. 1,2,3 B. 4,5,9 C. 4,6,8 D. 5,5,11
-
科目: 来源: 题型:
查看答案和解析>>【题目】将内直径为20cm的圆柱形水桶中的全部水倒入一个长、宽、高分别为30cm,20cm,62.8cm的长方体铁盒中,正好倒满,求圆柱形水桶的高.(π取3.14)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(备注:在直角三角形中30度角所对的边是斜边的一半)
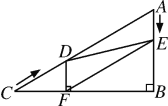
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,确定事件是( )
A. 早晨太阳从西方升起
B. 打开电视机,它正在播动画片
C. 掷一枚硬币,正面向上
D. 任意买一张电影票,座位号是2的倍数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种流感病毒的直径是0.00000008m,这个数据用科学记数法表示为( )
A.8×10﹣6m
B.8×10﹣5m
C.8×10﹣8m
D.8×10﹣4m
相关试题

