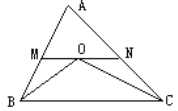
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交与点O, 过点O作MN∥BC,若AB=6,AC=9,则△AMN的周长为_____________。
参考答案:
【答案】15
【解析】先根据角平分线的性质和平行线判断出OM=BM、ON=CN,也就得到三角形的周长就等于AB与AC的长度之和.
解:如图,
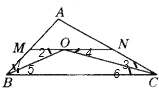
∵OB、OC分别是∠ABC与∠ACB的平分线,
∴∠1=∠5,∠3=∠6,
又∵MN∥BC,∴∠2=∠5,∠6=∠4,
∴BM=MO,NO=CN,
∴△AMN的周长=AM+AN+MN=MA+AN+MO+ON=AB+AC,
又∵AB=6,AC=9,
∴△AMN的周长=6+9=15.
故答案为:15.
“点睛”本题考查了等腰三角形的性质;解答此题的关键是熟知平行线的性质,等腰三角形的性质及角平分线的性质及利用线段的等量代换.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x的2倍与3的差可表示为___________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是方程2x2﹣3x﹣m=0的一个根,则m的值为( )
A. 1 B. 5 C. -1 D. -5
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(m﹣1)x2﹣x+m2﹣1=0的一个解是0,则m的值为( )
A. 0 B. ±1 C. 1 D. -1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=(k﹣2)x+k经过第一、二、四象限,则k的取值范围是( )
A.k≠2B.k>2C.0<k<2D.0≤k<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且
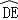 =
=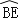 .
.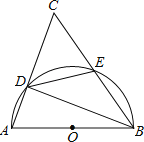
(1)试判断△ABC的形状,并说明理由.
(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+bx+C的图象过点A(﹣3,0),C(0,3).
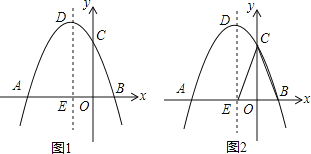
(1)求抛物线的解析式;
(2)探究:在抛物线的对称轴DE上是否存在点P,使得点P到直线AD和到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)探究:在对称轴DE左侧的抛物线上是否存在点F,使得2S△FBC=3S△EBC?若存在,求出点F的坐标;若不存在,说明理由.
相关试题

