【题目】如图,在第一个△ABA1中∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,则以点A4为顶点的等腰三角形的底角的度数为( )

A. 175° B. 170° C. 10° D. 5°
参考答案:
【答案】D
【解析】
先根据等腰三角形的性质求出∠BA1A的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠CA2A1,∠DA3A2及∠EA4A3的度数,找出规律即可得出∠A6的度数.
∵在△ABA1中,∠B=20°,AB=A1B,
∴∠BA1A=![]() =80°,
=80°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1=![]() =40°;
=40°;
同理可得∠DA3A2=20°,∠EA4A3=10°,
∴∠An=![]() ,
,
以点A4为顶点的底角为∠A5.
∵∠A5=![]() =5°,
=5°,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(理解新知)
如图①,已知
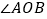 ,在
,在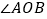 内部画射线
内部画射线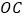 ,得到三个角,分别为
,得到三个角,分别为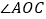 、
、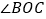 、
、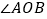 ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线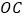 为
为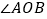 的“2倍角线”
的“2倍角线”(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若
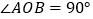 ,射线
,射线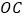 为
为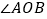 的“2倍角线”,则
的“2倍角线”,则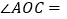
 ;
;(解决问题)
如图②,已知
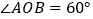 ,射线
,射线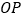 从
从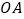 出发,以每秒
出发,以每秒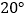 的速度绕
的速度绕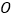 点逆时针旋转:射线
点逆时针旋转:射线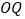 从
从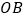 出发,以每秒
出发,以每秒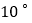 的速度绕
的速度绕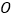 点顺时针旋转,射线
点顺时针旋转,射线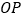 、
、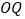 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为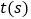 .
.(3)当射线
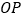 、
、 旋转到同一条直线上时,求
旋转到同一条直线上时,求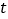 的值;
的值;(4)若
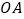 、
、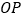 、
、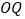 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的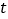 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于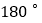 的角.)
的角.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;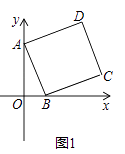
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C是不在同一条直线上的三点,请按下列要求画图并作答(画图时工具不限,不需写出结论,只需画出图形、标注字母):
(1)画直线BC,连接AC;
(2)画线段BC的中点D,连接AD;
(3)画出∠ADC的平分线交AC于点E;
(4)若∠BDA=
 求∠ADC,∠EDC.
求∠ADC,∠EDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=kx2﹣7x﹣7的图象与x轴有两个交点,则k的取值范围为( )
A.k>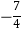
B.k>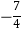 且k≠0
且k≠0
C.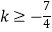
D.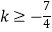 且k≠0
且k≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 .

相关试题

