【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为 . 
参考答案:
【答案】3
【解析】∵四边形ABCD是矩形,
∴BD=AC,即当AC最小时,BD就最小;
∵在抛物线 ![]() 中,顶点(1,3)距离
中,顶点(1,3)距离 ![]() 轴最近,
轴最近,
∴当点A运动到抛物线的顶点时,AC最短为3,
∴BD的最小值为3.
【考点精析】根据题目的已知条件,利用二次函数的性质和二次函数的最值的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个△ABA1中∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,则以点A4为顶点的等腰三角形的底角的度数为( )

A. 175° B. 170° C. 10° D. 5°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=kx2﹣7x﹣7的图象与x轴有两个交点,则k的取值范围为( )
A.k>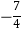
B.k>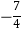 且k≠0
且k≠0
C.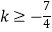
D.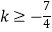 且k≠0
且k≠0 -
科目: 来源: 题型:
查看答案和解析>>【题目】点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线l:y=
 (x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.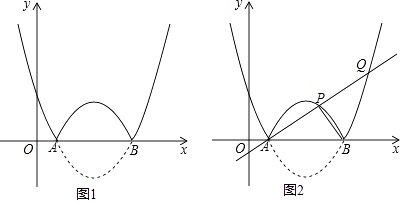
(1)若点A的坐标为(1,0).
①求抛物线l的表达式,并直接写出当x为何值时,函数的值y随x的增大而增大;
②如图2,若过A点的直线交函数的图象于另外两点P,Q,且S△ABQ=2S△ABP , 求点P的坐标;
(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AD=8cm,AB=6cm.动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是下图中的( )
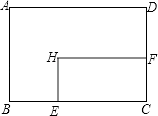
A.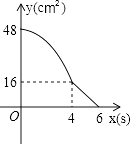
B.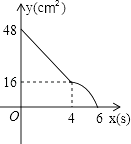
C.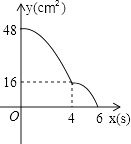
D.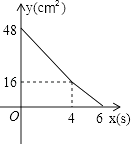
-
科目: 来源: 题型:
查看答案和解析>>【题目】报社需要在40分钟内将一篇紧急宣传文稿输入电脑.已知独立完成此项任务,小王需要50分钟,小李只需要30分钟.小王独自输入了30分钟后,因为急于完成任务,请求小李帮助他(求助时间忽略不计),他们能在要求的时间内完成任务吗?请说明理由.
相关试题

