Question

【题目】如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）
A.
B.2
C.
D.

Answer 1

【答案】B
【解析】解：∵∠ABC=90°， ∴∠ABP+∠PBC=90°，
∵∠PAB=∠PBC，
∴∠BAP+∠ABP=90°，
∴∠APB=90°，
∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，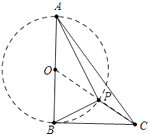

此时PC最小，
在RT△BCO中，∵∠OBC=90°，BC=4，OB=3，
∴OC= =5，
∴PC=OC﹣OP=5﹣3=2．
∴PC最小值为2．
故选B．
【考点精析】关于本题考查的圆周角定理和点和圆的三种位置关系，需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；圆和点的位置关系：以点P与圆O的为例（设P是一点，则PO是点到圆心的距离），P在⊙O外，PO＞r；P在⊙O上，PO＝r；P在⊙O内，PO＜r才能得出正确答案．