【题目】如图,P是Rt△ABC的斜边BC上异于B,C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
A.1条
B.2条
C.3条
D.4条
参考答案:
【答案】C
【解析】因为截得的三角形与△ABC相似,而截得的三角形与原三角形已有一个公共角,所以只要再作一个直角就可以.如图,过点M作AB的垂线,或作AC的垂线,或作BC的垂线,
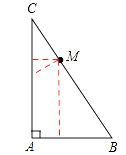
所得三角形都满足题意.即满足条件的直线共有三条.
所以答案是:C.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树
 他先让爸爸开车驶过这段公路,发现速度为60千米
他先让爸爸开车驶过这段公路,发现速度为60千米 小时,走了约3分钟,由此估算这段路长约______千米.
小时,走了约3分钟,由此估算这段路长约______千米.然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米
 小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵数,请你求出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有 .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得 = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: + =( +
,填空: + =( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正△ABC中,D,E分别在AC,AB上,且
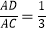 ,AE=BE,则有( )
,AE=BE,则有( )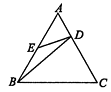
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD -
科目: 来源: 题型:
查看答案和解析>>【题目】丫头和爸爸从家出发到大剧院观看“巴交有声”巴蜀中学新年演奏会,爸爸先出发,2分钟后丫头沿同一路线出发去追爸爸,当丫头追上爸爸时发现背包落在途中了,爸爸立即返回找背包,丫头继续前往大剧院,当丫头到达大剧院时,爸爸刚好找到背包并立即前往大剧院
 爸爸找背包的时间不计
爸爸找背包的时间不计 ,丫头在大剧院等了一会,没有等到爸爸,就沿同一路线返回接爸爸,最终与爸爸会合,丫头和爸爸的速度始终不变,如图是丫头和爸爸两人之间的距离
,丫头在大剧院等了一会,没有等到爸爸,就沿同一路线返回接爸爸,最终与爸爸会合,丫头和爸爸的速度始终不变,如图是丫头和爸爸两人之间的距离 米
米 与丫头出发的时间
与丫头出发的时间 分钟
分钟 的函数图象,则丫头在大剧院等了爸爸______分钟.
的函数图象,则丫头在大剧院等了爸爸______分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为 ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D.“抛一枚正方体骰子,朝上的点数为2的概率为 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在  附近
附近 -
科目: 来源: 题型:
查看答案和解析>>【题目】真假命题的思考.
一天,老师在黑板上写下了下列三个命题:
①垂直于同一条直线的两条直线平行;
②若
 ,则
,则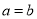
③若
 和
和 的两边所在直线分别平行,则
的两边所在直线分别平行,则 .
.小明和小丽对话如下,
小明:“命题①是真命题,好像可以证明.”
小丽:“命题①是假命题,好像少了一些条件.”
(1)结合小明和小丽的对话,谈谈你的观点.如果你认为是真命题,请证明:如果你认为是假命题,请增加一个适当的条件,使之成真命题.
(2)请在命题②、命题③中选一个,如果你认为它是真命题,请证明:如果你认为它是假命题,请举出反例.
相关试题

