【题目】如图,ABC中,AB=AC=4![]() ,cosC=
,cosC=![]() .
.
(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法).
(2)综合应用:在你所作的圆中,求证: ![]() ;
;
(3)求△BDE的周长.

参考答案:
【答案】(1)作图见解析;(2)证明见解析;(3)△BDE的周长为8+![]() .
.
【解析】试题分析:做AC的中垂线得出圆心的位置;(2)连接AE,根据直径的性质得出∠AEC=∠AEB=90°,根据AB=AC得出∠BAE=∠CAE,从而得出∠CAE=∠BAE,得出弧相等;(3)根据Rt△ACE的三角形函数得出CE的长度,根据(2)得出BE=CE=DE=4,根据Rt△BCD中∠B的三角函数得出BC和BD的长度,从而得出三角形周长.
试题解析:(1)如图1,⊙O为所求.
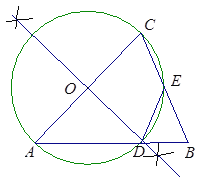
(2)证明:如图,连接AE, ∵AC为⊙O的直径,点E在⊙O上,∴∠AEC=90°,
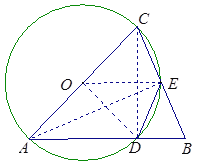
∵AB=AC,∴∠BAE =∠CAE, ∴![]() .
.
(3)解:如图在Rt△ACE中,
![]() ,
, ![]() ,∴
,∴![]() .
.
∵AB= AC,∠AEC=90°,∴∠B =∠ACB,BE= CE=4. 又![]()
![]() ,∴DE= CE=4.
,∴DE= CE=4.
在Rt△BCD中, ![]() , ∵
, ∵![]() ,BC=8,
,BC=8,
∴![]() ,
,
∴![]() 的周长
的周长![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+
 x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.
x+c过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB.过点B作x轴的垂线、过点A作y轴的垂线,两直线相交于点D.(1)求此抛物线的对称轴;
(2)当t为何值时,点D落在抛物线上?
(3)是否存在t,使得以A、B、D为顶点的三角形与△PEB相似?若存在,求此时t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式5x﹣1>2x+5的解集为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度可能为( )
A. 先右转50°,后右转40°B. 先右转50°,后左转40°
C. 先右转50°,后左转130°D. 先右转50°,后左转50°
-
科目: 来源: 题型:
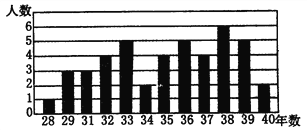
查看答案和解析>>【题目】菲尔兹奖(The International Medals for Outstanding Discoveries in Mathematics)是国际数学联盟的国际数学家大会上颁发的奖项。每四年一次颁给有卓越贡献的年轻数学家,得奖者须在该年元旦前未满四十岁。菲尔兹奖被视为数学界的诺贝尔奖。本题中给出的条形图是截止到2002年44位费尔兹奖得主获奖时的年龄统计图。经计算菲尔兹奖得主获奖时的平均年龄是35岁。请根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时年龄的众数是多少?
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,若点A(﹣2,n),B(1,﹣2)是一次函数y=kx+b的图象和反比例函数y=
 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标;
(3)求点O到直线AB的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的为( )
A. 在同一平面内,不重合的两条直线不相交就平行B. 若a2=b2,则a=b
C. 若x=y,则|x|=|y|D. 同角的补角相等
相关试题

