【题目】如图,经过点A(0,﹣4)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.
x2+bx+c与x轴相交于点B(﹣1,0)和C,O为坐标原点.

(1)求抛物线的解析式;
(2)将抛物线y=![]() x2+bx+c向上平移
x2+bx+c向上平移![]() 个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
个单位长度,再向左平移m(m>0)个单位长度,得到新抛物线,若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)将x轴下方的抛物线图象关于x轴对称,得到新的函数图象C,若直线y=x+k与图象C始终有3个交点,求满足条件的k的取值范围.
参考答案:
【答案】(1)、y=![]() ;(2)、
;(2)、![]() <m<
<m<![]() ;(3)、1或
;(3)、1或![]()
【解析】
试题分析:(1)、该抛物线的解析式中只有两个待定系数,只需将A、B两点坐标代入即可得解.(2)、首先根据平移条件表示出移动后的函数解析式,进而用m表示出该函数的顶点坐标,将其代入直线AB、AC的解析式中,即可确定P在△ABC内时m的取值范围.(3)、先根据函数解析式画出图形,然后结合图形找出抛物线与x轴有三个交点的情形,最后求得直线的解析式,从而可求得m的值.
试题解析:(1)、∵经过点A(0,﹣4)的抛物线y=![]() x2+bx+c与x轴相交于点B(﹣1,0),
x2+bx+c与x轴相交于点B(﹣1,0),
∴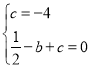 , ∴
, ∴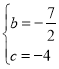 , ∴抛物线解析式为y=
, ∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣4,
x﹣4,
(2)、由(1)知,抛物线解析式为y![]() x2﹣
x2﹣![]() x﹣4=
x﹣4=![]() (x2﹣7x)﹣4=
(x2﹣7x)﹣4=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴此抛物线向上平移![]() 个单位长度的抛物线的解析式为y=
个单位长度的抛物线的解析式为y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
再向左平移m(m>0)个单位长度,得到新抛物线y=![]() (x+m﹣
(x+m﹣![]() )2﹣
)2﹣![]() ,
,
∴抛物线的顶点P(﹣m+![]() ,﹣
,﹣![]() ), 对于抛物线y=
), 对于抛物线y=![]() x2﹣
x2﹣![]() x﹣4,令y=0,
x﹣4,令y=0,![]() x2﹣
x2﹣![]() x﹣4=0,解得x=﹣1或8, ∴B(8,0),∵A(0,﹣4),B(﹣1,0),
x﹣4=0,解得x=﹣1或8, ∴B(8,0),∵A(0,﹣4),B(﹣1,0),
∴直线AB的解析式为y=﹣4x﹣4,直线AC的解析式为y=![]() x﹣4, 当顶点P在AB上时,﹣
x﹣4, 当顶点P在AB上时,﹣![]() =﹣4×(﹣m+
=﹣4×(﹣m+![]() )﹣4,解得m=
)﹣4,解得m=![]() , 当顶点P在AC上时,﹣
, 当顶点P在AC上时,﹣![]() =
=![]() (﹣m+
(﹣m+![]() )﹣4,
)﹣4,
解得m=![]() , ∴当点P在△ABC内时
, ∴当点P在△ABC内时![]() <m<
<m<![]() .
.
(3)、翻折后所得新图象如图所示.
平移直线y=x+k知:直线位于l1和l2时,它与新图象有三个不同的公共点.
①当直线位于l1时,此时l1过点B(﹣1,0), ∴0=﹣1+k,即k=1.
②∵当直线位于l2时,此时l2与函数y=﹣![]() x2+
x2+![]() x+4(﹣1≤x≤8)的图象有一个公共点
x+4(﹣1≤x≤8)的图象有一个公共点
∴方程x+k=﹣![]() x2+
x2+![]() x+4,即x2﹣5x﹣8+2k=0有两个相等实根. ∴△=25﹣4(2k﹣8)=0,即k=
x+4,即x2﹣5x﹣8+2k=0有两个相等实根. ∴△=25﹣4(2k﹣8)=0,即k=![]() .
.
综上所述,k的值为1或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据21、12、18、16、20、21的众数和中位数分别是( )
A.21和19
B.21和17
C.20和19
D.20和18 -
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:(1)三角形具有稳定性;(2)有两边和一个角分别相等的两个三角形全等(3)三角形的外角和是180°(4)全等三角形的面积相等.其中正确的个数是 ( ).
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )
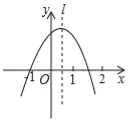
A.①③ B.②③ C.②④ D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】用不等式表示: x与5的差不小于x的2倍:________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两条边长分别为3cm和6cm,则它的周长为_____________cm.
相关试题

