【题目】两个大小不同的等腰直角三角形三角板如图![]() 所示放置,图
所示放置,图![]() 是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
是由它抽象出的几何图形,B,C,E在同一条直线上,联结DC,
![]() 请找出图
请找出图![]() 中的全等三角形,并给予说明
中的全等三角形,并给予说明![]() 说明:结论中不得含有未标识的字母
说明:结论中不得含有未标识的字母![]() ;
;
![]() 试说明:
试说明:![]() .
.

参考答案:
【答案】⑴△![]() ≌△
≌△![]() 证明略 ⑵略
证明略 ⑵略
【解析】
试题①可以找出△BAE≌△CAD,条件是AB=AC,DA=EA,∠BAE=∠DAC=90°+∠CAE.
②由①可得出∠DCA=∠ABC=45°,则∠BCD=90°,所以DC⊥BE.
解:(1)∵△ABC,△DAE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°.
∠BAE=∠DAC=90°+∠CAE,
在△BAE和△DAC中

∴△BAE≌△CAD(SAS).
(2)由(1)得△BAE≌△CAD.
∴∠DCA=∠B=45°.
∵∠BCA=45°,
∴∠BCD=∠BCA+∠DCA=90°,
∴DC⊥BE.
-
科目: 来源: 题型:
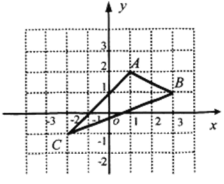
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
⑴.在图中作出△ABC关于y轴对称的△A1B1C1.
⑵.写出点A1,B1,C1的坐标(直接写出答案).
A1 B1 C1 ;
⑶.△A1B1C1的面积为 .
-
科目: 来源: 题型:
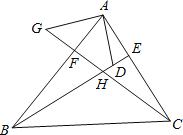
查看答案和解析>>【题目】如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①.AD=BC;②.DE=CF;③.BE∥AF.
⑴.请用其中两个关系式作为条件,另一个作为结论,写出所有正确的结论.
⑵.选择(1)中你写出的一个正确结论,说明它正确的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.试猜想线段AD与AG的数量及位置关系,并证明你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个安装有进出水管的30升容器,水管每单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量
 (升)与时间
(升)与时间 (分)之间的函数关系如图所示.根据图象回答下列问题:
(分)之间的函数关系如图所示.根据图象回答下列问题:(1)求每分钟进水多少升;
(2)若12分钟后只放水,不进水,求需要多长时间可以把水放完;
(3)若从一开始进出水管同时打开,求需要多长时间可以将容器灌满。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC的三个顶点的坐标为A(1,0),B(6,0),C(3,-4).
(1)求△ABC的面积
(2)若A,B两点的位置不变,点P在
 轴什么位置时,
轴什么位置时, 的面积是
的面积是 面积的2倍;
面积的2倍;(3)若A,B两点的位置不变,点P在
 轴什么位置时,
轴什么位置时, 的面积是
的面积是 面积的2倍;
面积的2倍;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
成绩(分)
46
47
48
49
50
人数(人)
1
2
1
2
4
下列说法正确的是( )
A.这10名同学的体育成绩的众数为50
B.这10名同学的体育成绩的中位数为48
C.这10名同学的体育成绩的方差为50
D.这10名同学的体育成绩的平均数为48
相关试题

