【题目】[数学实验探索活动]
实验材料现有若干块如图①所示的正方形和长方形硬纸片.

实验目的:
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,得到相应的等式,从而探求出多项式乘法或分解因式的新途径.
例如,选取正方形、长方形硬纸片共 6 块,拼出一个如图②的长方形,计算它的面积, 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2.
问题探索:
(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ,那么需要两种正方形纸片 张,长方形纸片 张;
(2)选取正方形、长方形硬纸片共 8 块,可以拼出一个如图③的长方形,计算图③的面积,并写出相应的等式;
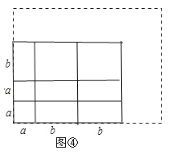
(3)试借助拼图的方法,把二次三项式 2a2+5ab+2b2 分解因式,并把所拼的图形画在虚线方框内.
参考答案:
【答案】(1)3,3;(2)a2+4ab+3b2=(a+3b)(a+b);(3)2b2+5ab+2a2=(2b+a)(b+2a).画图见解析.
【解析】
(1)根据多项式(2a+b)(a+b) =2a2+3ab+b2可发现矩形有两个小正方形,一个大正方形和三个小长方形.
(2)正方形、长方形硬纸片一共八块,面积等于长为a+3b,宽为a+b的矩形面积.所以a2+4ab+3b2=(a+3b)(a+b)
(3)正方形、长方形硬纸片共9块,画出图形,面积等于长为a+2b,宽为2a+b的矩形面积,则2a2+5ab+2b2=(2a+b)(a+2b)
(1)∵(2a+b)(a+b) =2a2+3ab+b2;
∴拼图需要两个小正方形,一个大正方形和三个小长方形
∴需要3个正方形纸片,3个长方形纸片.
(2)∵大长方形长为a+3b,宽为a+b
∴面积S=(a+3b)(a+b)
又∵大长方形由三个大正方形,一个小正方形和四个小长方形组成
∴面积S= a2+4ab+3b2
∴a2+4ab+3b2=(a+3b)(a+b)
(3)∵由2b2+5ab+2a2可知
大长方形由两个小正方形和两个大正方形以及五个长方形组成,如图
∴2b2+5ab+2a2=(2b+a)(b+2a).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某广场内有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,
 ,
, ,
, ,
, ,
, 求四边形ABCD空地的面积.
求四边形ABCD空地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:
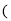 总利润
总利润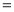 单件利润
单件利润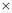 销售量
销售量
商品价格
A
B
进价
 元
元 件
件
1200
1000
售价
 元
元 件
件
1350
1200
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原进价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原售价销售,而B商品按原售价打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年9月29日,由北京外交人员服务局主办、北京外交人员房屋服务公司、北京市乒乓球运动协会承办的首届中外外交官“友谊杯”乒乓球赛在北京齐家园外交公寓体育运动中心举办,为了纪念这次活动,某校开展了乒乓球知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其成绩如图所示:

 根据上图填写下表:
根据上图填写下表:平均数
中位数
众数
甲班

______

乙班
______
8
______
 已知甲班5名同学成绩的方差是
已知甲班5名同学成绩的方差是 ,计算乙班同学成绩的方差,并比较哪个班选手的成绩较为稳定?
,计算乙班同学成绩的方差,并比较哪个班选手的成绩较为稳定? -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省市先后出台了居民用电“阶梯价格”制度,下表是某市的电价标准(每月).
阶梯
一户居民每月用电量x(单位:度)
电费价格(单位:元/度)
一档
0<x≤180
a
二档
180<x≤280
b
三档
x>280
0.82
(1)已知小华家四月份用电200度,缴纳电费105元;五月份用电230度,缴纳电费122.1元,请你根据以上数据,求出表格中a,b的值;
(2)六月份是用电高峰期,小华家计划六月份电费支出不超过208元,那么小华家六月份最多可用电多少度?
相关试题

