搜索
【题目】在某中学举行的演讲比赛中，八年级5名参赛选手的成绩如下表所示
选手 | 1号 | 2号 | 3号 | 4号 | 5号 |
得分 | 92 | 95 | 91 | 89 | 88 |
（1）计算出这5名选手的平均成绩；
（2）计算出这5名选手成绩的方差．
参考答案：
【答案】解：（1）
=（95+91+89+88）÷5=91；
（2）S2=
（92﹣91）2+（95﹣91）2+（91﹣91）2+（89﹣91）2+（88﹣91）2=6．
【解析】（1）先求出5个选手的得分和，再除以51求平均数即可；
（2）利用方差公式S2=
[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]计算即可．
【考点精析】关于本题考查的算术平均数，需要了解总数量÷总份数=平均数．解题关键是根据已知条件确定总数量以及与它相对应的总份数才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，连接CD.过点C作CE⊥DB，垂足为E，直线AB与CE相交于F点.
（1）求证：CF为⊙O的切线；
（2）当BF=5,
时，求BD的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果|m﹣3|+(n+2)2＝0，那么mn的值是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知4n﹣m=4，则（m﹣4n）2﹣3（m﹣4n）﹣10的值是（ ）
A.﹣6
B.6
C.18
D.﹣38 -
科目： 来源： 题型：
查看答案和解析>>【题目】若一个多边形除了一个内角外，其余各内角之和为2570°，求这个内角的度数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究题：
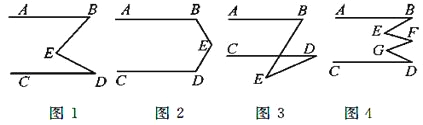
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗？
(2)若将点E移至图2的位置,此时∠B，∠D，∠E之间有什么关系？
(3)若将点E移至图3的位置,此时∠B，∠D，∠E之间的关系又如何？
(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系？
-
科目： 来源： 题型：
查看答案和解析>>【题目】三角形三个内角的度数分别是（x+y）°，（x-y）°，x°，且x＞y＞0，则该三角形有一个内角为（ ）
A. 30°
B. 45°
C. 90°
D. 60°
相关试题
