【题目】如图(单位:cm).等腰直角△ABC以2cm/s的速度沿着直线![]() 向正方形移动,直到AB与CD重合.设x秒时,三角形与正方形重叠部分的面积为ycm2.
向正方形移动,直到AB与CD重合.设x秒时,三角形与正方形重叠部分的面积为ycm2.
⑴写出y与x的关系式;
⑵当x=3.5时,y是多少;
⑶当重叠部分的面积是正方形面积的一半时,三角形移动了多少时间;
⑷正方形边长改为30cm,等腰直角三角形大小不变,移动到AB与EF重合为止.
①x的取值范围是 ;
②当x满足 时,y=50;
③写出当15≤x≤20时,y与x的关系式.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)①
;(4)①![]() ;②
;②![]() ;
;
③当![]() 时,
时,![]()
【解析】
(1)根据题意可知,三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,据此可得出y、x的函数关系式;
(2)可将x的值,代入(1)的函数关系式中,即可求得y的值;
(3)将正方形的面积的一半代入(1)的函数关系式中,即可求得x的值.
(4)根据三角形与正方形重叠部分的情况分类讨论即可得到答案.
解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以![]() ;
;
(2)在![]() 中, 当x=3.5时,
中, 当x=3.5时,![]() ;
;
(3)在![]() 中 因为当y=50时,
中 因为当y=50时,![]()
所以![]() x=5秒(负值舍去).
x=5秒(负值舍去).
(4)①运动时间的起点为![]() 当
当![]() 与
与![]() 重合时,时间
重合时,时间![]()
所以![]() 的取值范围是
的取值范围是![]()
②如图,当![]() 此时三角形运动在正方形的内部,
此时三角形运动在正方形的内部,
当![]() 与
与![]() 重合时,
重合时,![]() ,
,
当![]() 与
与![]() 重合时,
重合时,![]()
![]()

③ 当![]() 时,如图,记
时,如图,记![]() 与
与![]() 的交点为
的交点为![]() ,
,
此时重叠部分的面积是直角梯形![]() 的面积,
的面积,

由题意知:![]() ,
,![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,E为CD边上一点,且AE、BE分别平分∠DAB、∠ABC.

(1)求证:△ADE≌△BCE;
(2)已知AD=3,求矩形的另一边AB的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:点C在线段BD上,AC⊥CE,∠A=∠1,∠E=∠2.
(1)若∠1=70°,求∠B、∠D的度数;
(2)判断AB与ED的位置关系,并说明理由;
(3)作∠A、∠E的角平分线相交于点P,求∠P的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】用下列边长相同的正多边形组合,能够铺满地面不留缝隙的是()
A. 正八边形和正三角形 B. 正五边形和正八边形
C. 正六边形和正三角形 D. 正六边形和正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形
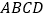 中,
中, 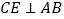 ,垂足为
,垂足为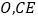 与
与 的延长线相交于
的延长线相交于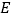 ,且
,且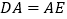 ,连接
,连接 ;
;(1)如图
 ,求证:四边形
,求证:四边形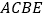 是菱形;
是菱形;(2)如图
 ,连接
,连接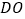 ,若
,若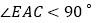 ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图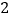 中所有面积等于
中所有面积等于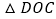 的面积的钝角三角形.
的面积的钝角三角形.
相关试题

