【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ![]() ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 ![]() CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
① ![]() CMP∽
CMP∽ ![]() BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当 ![]() ABP≌
ABP≌ ![]() AND时,BP=4
AND时,BP=4 ![]() -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
参考答案:
【答案】D
【解析】解: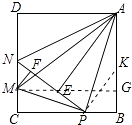 ∵∠APB=∠APE,∠MPC=∠MPN,
∵∠APB=∠APE,∠MPC=∠MPN,
∵∠CPN+∠NPB=180°,
∴2∠NPM+2∠APE=180°,
∴∠MPN+∠APE=90°,
∴∠APM=90°,
∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,
∴∠CPM=∠PAB,
∵四边形ABCD是正方形,
∴AB=CB=DC=AD=4,∠C=∠B=90°,
∴△CMP∽△BPA.故①正确,
设PB=x,则CP=4-x,
∵△CMP∽△BPA,
∴![]() =
=![]() ,
,
∴CM=![]() x(4-x),
x(4-x),
∴S四边形AMCB=![]() [4+
[4+![]() x(4-x)]×4=-
x(4-x)]×4=-![]() x2+2x+8=-
x2+2x+8=-![]() (x-2)2+10,
(x-2)2+10,
∴x=2时,四边形AMCB面积最大值为10,故②正确,
易证得△ADN≌△AEN,当PB=PC=PE=2时,设ND=NE=y,
在RT△PCN中,(y+2)2=(4-y)2+22解得y=![]() ,
,
∴NE≠EP,故③错误,
作MG⊥AB于G,
∵AM=![]() =
=![]() ,
,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=4-![]() x(4-x)=
x(4-x)=![]() (x-2)2+3,
(x-2)2+3,
∴x=2时,AG最小值=3,
∴AM的最小值=![]() =5,故④错误.
=5,故④错误.
∵△ABP≌△ADN时,
∴∠PAB=∠DAN=22.5°,在AB上取一点K使得AK=PK,设PB=z,
∴∠KPA=∠KAP=22.5°
∵∠PKB=∠KPA+∠KAP=45°,
∴∠BPK=∠BKP=45°,
∴PB=BK=z,AK=PK=![]() z,
z,
∴z+![]() z=4,
z=4,
∴z=4![]() -4,
-4,
∴PB=4![]() -4,故⑤正确.
-4,故⑤正确.
故正确的为①②⑤.
故选D.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度数.
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
(x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=
 .
. 
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,选段AB=4,以AB为直径作半圆O,点C为弧AB的中点,点P为直径AB上一点,联结PC,过点C作CD∥AB,且CD=PC,过点D作DE∥PC,交射线PB于点E,PD与CE相交于点Q.

(1)若点P与点A重合,求BE的长;
(2)设PC=x, =y,当点P在线段AO上时,求y与x的函数关系式及定义域;
=y,当点P在线段AO上时,求y与x的函数关系式及定义域;
(3)当点Q在半圆O上时,求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABC中,AD平分
ABC中,AD平分 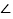 BAC,按如下步骤作图:
BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧做弧,交于两点M、N;
AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).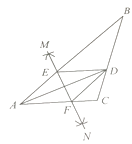
A.2
B.4
C.6
D.8
相关试题

