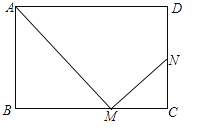
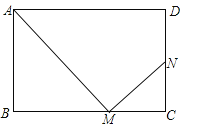
【题目】在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
参考答案:
【答案】(1)证明见试题解析;(2)![]() ,当x=
,当x=![]() 时,y取最大值,为
时,y取最大值,为![]() ;(3)b=2a.
;(3)b=2a.
【解析】
试题分析:(1)由矩形的性质可得∠B=∠C=90°,要证△CMN∽△BAM,只需证∠BAM=∠CMN即可;
(2)由△CMN∽△BAM即可得到y与x的函数解析式,然后只需运用配方法就可求出y的最大值;
(3)由点M在BC上运动(点M与点B、C不重合),可得0<x<b,要满足条件①,应保证当0<x<b时,y≤a恒成立,要满足条件②,需存在一个x,使得y=a,综合条件①和②,当0<x<b时y最大值应为a,然后结合(2)中的结论,就可解决问题.
试题解析:(1)∵四边形ABCD是矩形,∴∠B=∠C=90°,∴∠BAM+∠AMB=90°.∵MN⊥AM,即∠AMN=90°,∴∠CMN+∠AMB=90°,∴∠BAM=∠CMN,∴△CMN∽△BAM;
(2)∵△CMN∽△BAM,∴![]() .∵BM=x,CN=y,AB=a,BC=AD=b,∴
.∵BM=x,CN=y,AB=a,BC=AD=b,∴![]() ,∴
,∴![]() =
=![]() .∵
.∵![]() <0,∴当x=
<0,∴当x=![]() 时,y取最大值,最大值为
时,y取最大值,最大值为![]() ;
;
(3)由题可知:当0<x<b时,y的最大值为a,即![]() =a,解得:b=2a.∴要同时满足两个条件,b的值为2a.
=a,解得:b=2a.∴要同时满足两个条件,b的值为2a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2b﹣2ab+b= .
-
科目: 来源: 题型:
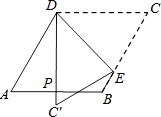
查看答案和解析>>【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )
A.78°
B.75°
C.60°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品涨价30%后欲恢复原价,则必须下降的百分数约为( )
A.20%
B.21%
C.22%
D.23% -
科目: 来源: 题型:
查看答案和解析>>【题目】某市人口数为190.1万人,用科学记数法表示该市人口数为( )
A.1.901×106人
B.19.01×105 人
C.190.1×104人
D.1901×103人 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l上有三点A、B、C,且AB=6,BC=4,M、N分别是线段AB、BC的中点,则MN= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个顶点的坐标分别是A(﹣2,3),点B(0,1),点C(2,2).
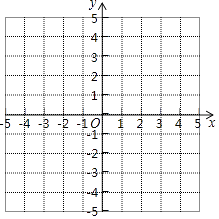
(1)在所给的平面直角坐标系中画出△ABC.
(2)直接写出点A到x轴,y轴的距离分别是多少?
(3)求出△ABC的面积.
相关试题

