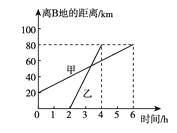
【题目】如图是甲骑自行车与乙骑摩托车分别从A,B两地向C地(A,B,C地在同一直线上)行驶过程中离B地的距离与行驶时间的关系图,请你根据图象回答下列问题:
(1)A,B两地哪个距C地近?近多少?
(2)甲、乙两人谁出发时间早?早多长时间?
(3)甲、乙两人在途中行驶的平均速度分别为多少?
参考答案:
【答案】(1)A地距C地近,近20km;(2)甲出发时间早,早2h;(3)甲的平均速度为10km/h,乙的平均速度为40km/h.
【解析】
(1)根据图象中,刚开始时,甲从A地出发,离B地的距离为![]() ,随着时间的增大,离B地的距离越远,从而可知A地在B、C两地的中间,由此即可得出答案;
,随着时间的增大,离B地的距离越远,从而可知A地在B、C两地的中间,由此即可得出答案;
(2)由乙的图象可知,前![]() ,乙离B地的距离为
,乙离B地的距离为![]() ,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,由此即可得出答案;
,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,由此即可得出答案;
(3)根据“速度![]() 路程
路程![]() 时间”即可得.
时间”即可得.
(1)由图象可知,刚开始时,甲从A地出发,离B地的距离为![]() ,随着时间的增大,离B地的距离越远
,随着时间的增大,离B地的距离越远
则A地在B、C两地的中间
故A地距C地近,近![]() ;
;
(2)由乙的图象可知,前![]() ,乙离B地的距离为
,乙离B地的距离为![]() ,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,说明甲已出发
,即在这段时间,乙未出发,由甲的图象可知,甲离B地的距离越来越远,说明甲已出发
故甲出发时间早,早![]() ;
;
(3)甲的平均速度为![]()
乙的平均速度为![]()
答:甲的平均速度为![]() ,乙的平均速度为
,乙的平均速度为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为( )
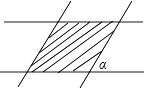
A.
B.
C.sinα
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
-
科目: 来源: 题型:
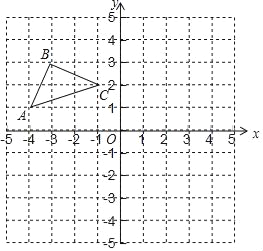
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中判断正确的有( )个.
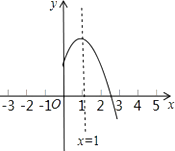
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2
 ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备购买A、B两种零件,已知A种零件的单价比B种零件的单价多30元,而用900元购买A种零件的数量和用600元购买B种零件的数量相等.
(1)求A、B两种零件的单价;
(2)根据需要,工厂准备购买A、B两种零件共200件,工厂购买两种零件的总费用不超过14700元,求工厂最多购买A种零件多少件?
相关试题

