【题目】由方程x﹢t=5,y﹣2t﹦4组成的方程组可得x,y的关系式是
A. x﹢y﹦9 B. 2x﹢y﹦7 C. 2x﹢y﹦14 D. x﹢y﹦3
参考答案:
【答案】C
【解析】由①得t=5-x,代入方程②,即可消去t得到关于x,y的关系式.
解:由①得:t=5-x,
再代入②得:y-2(5-x)=4,
即x+y=14.
故答案为:x+y=14.
“点睛”本题考查了代入消元法解方程组,是一个基础题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠A-∠B=∠C,则△ABC是______三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
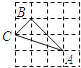
A.
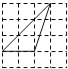 B.
B. 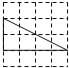 C.
C. 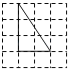 D.
D. 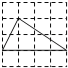
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x2-px+3)(x-2)的乘积中不含x2项,则()
A. p=2 B. p=±2 C. p=-2 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系.
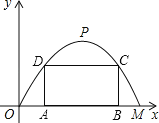
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD﹣DC﹣CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交线段BC于点E,设AP=x.
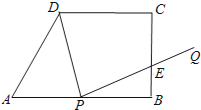
(1)当x为何值时,△APD是等腰三角形?
(2)若设BE=y,求y关于x的函数关系式;
(3)若BC的长a可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若不存在,请说明理由;若存在,写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C,并求出相应的AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
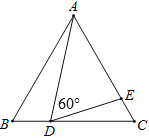
(1)求证:△ABD∽△DCE;
(2)如果AB=3,EC=
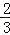 ,求DC的长.
,求DC的长.
相关试题

