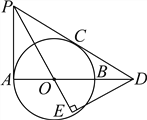
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=![]() ,求OE的长.
,求OE的长.
参考答案:
【答案】(1)证明见解析;(2) OE=![]() .
.
【解析】试题分析:(1)根据切线长定理和切线的性质即可证明:∠EPD=∠EDO;
(2)连接OC,利用tan∠PDA=![]() ,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.
,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.
试题解析:(1)证明:PA,PC与⊙O分别相切于点A,C,
∴∠APO=∠EPD且PA⊥AO,
∴∠PAO=90°,
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠EDO,
∴∠EPD=∠EDO;
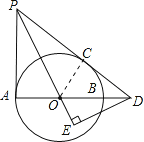
(2)解:连接OC,
∴PA=PC=6,
∵tan∠PDA=![]() ,
,
∴在Rt△PAD中,AD=8,PD=10,
∴CD=4,
∵tan∠PDA=![]() ,
,
∴在Rt△OCD中,OC=OA=3,OD=5,
∵∠EPD=∠ODE,
∴△OED∽△DEP,
∴![]() ,
,
∴DE=2OE
在Rt△OED中,OE2+DE2=OD2,即5OE2=52,
∴OE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

-
科目: 来源: 题型:
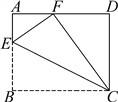
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为___.
-
科目: 来源: 题型:
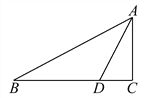
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠C=90°,D是BC边上一点,AC=6,CD=3,∠ADC=α.
(1)试写出α的正弦、余弦、正切这三个函数值;
(2)若∠B与∠ADC互余,求BD及AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1),规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次交换,如此这样,连续经过2 020次变换后,正方形ABCD的对角线交点M的坐标变为_________

-
科目: 来源: 题型:
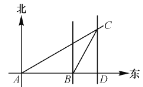
查看答案和解析>>【题目】如图,已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时30海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行1.5小时到达小岛C的正南方D点.求船从A到D一共走了多少海里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE
求证:(1)△ABC是等腰三角形
(2)当∠A=90°时,试判断四边形AFDE是怎样的四边形,证明你的结论

相关试题

