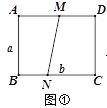
【题目】如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连接MN.
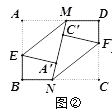
(1)如图②,分别沿ME、NF 将MN两侧纸片折叠,使点A、C分别落在MN上的A′、C′处,直接写出ME与FN的位置关系;
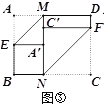
(2)如图③,当MN⊥BC 时,仍按(1)中的方式折叠,请求出四边形A′EBN与四边形C′FDM 的周长(用含a的代数式表示),并判断四边形A′EBN与四边形C′FDM周长之间的数量关系;
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系.

参考答案:
【答案】(1)EM∥NF ;(2)![]() 的周长与
的周长与![]() 的周长相等;(3)
的周长相等;(3)![]()
【解析】(1)先根据翻折变换的性质得到∠EMN=![]() ∠AMN,∠FNC′=
∠AMN,∠FNC′=![]() ∠MNC,再由平行线的性质可得到∠AMN=∠MNC,由平行线的判定定理即可得到ME∥FN;
∠MNC,再由平行线的性质可得到∠AMN=∠MNC,由平行线的判定定理即可得到ME∥FN;
(2)由折叠得知:A′E=AE,根据四边形A′EBN是矩形,即可求出四边形A′EBN的即四边形C′FDM的周长;
(3)根据折叠的性质可知OD=CD=OB=a,在△BCD中利用勾股定理即可求出b的值.
(1)EM∥NF ;
(2)∵矩形ABCD,
∴∠A=90°=∠B,
∵△AEM沿EM折叠到△![]()
∴∠![]() ,AE=
,AE=![]()
∵MN⊥BC,
∴∠MNB=90°,
∴有矩形![]() ,
,
∴其周长为![]() ,
,
同理 四边形![]() 也为矩形,周长为,
也为矩形,周长为,
![]() ,
,
∴![]() 的周长与
的周长与![]() 的周长相等;
的周长相等;
(3)∵四边形BNDM是菱形,
∴BM=MD,BD⊥MN,BO=DO,MO=NO,∠MBO=∠NBO,
∵△ABM沿BM折叠到△OBM,
∴AB=OB,AM=MO,∠ABM=∠OBM,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠MBO=30°,
在Rt△MBO中,∠MOB=90°,
∴BM=2MO,
设MO=x,BM=2x,
BO=![]()
AD=AM+MD=BM+MO=3x
∴![]() ,即
,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
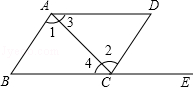
A.∠D+∠DAB=180°
B.∠B=∠DCE
C.∠1=∠2.
D.∠3=∠4 -
科目: 来源: 题型:
查看答案和解析>>【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:

(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来;
(3)如何分派才能使这50台联合收割机每天获得的租金最高?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某“希望学校”修建了一栋4层的教学大楼,每层楼有6间教室,进出这栋大楼共有3道门(两道大小相同的正门和一道侧门).安全检查中,对这3道门进行了测试:当同时开启一道正门和一道侧门时,2分钟内可以通过400名学生,若一道正门平均每分钟比一道侧门可多通过40名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%.安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这3道门安全撤离.假设这栋教学大楼每间教室最多有45名学生,问:建造的这3道门是否符合安全规定?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
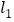 的解析表达式为
的解析表达式为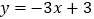 ,且
,且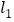 与
与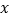 轴交于点
轴交于点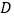 .直线
.直线 经过点
经过点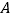 、
、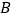 ,直线
,直线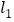 ,
, 交于点
交于点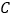 .
.(1)求点
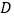 的坐标;
的坐标;(2)求直线
 的解析表达式;
的解析表达式;(3)求
 的面积;
的面积;(4)在直线
 上存在异于点
上存在异于点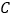 的另一个点
的另一个点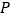 ,使得
,使得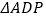 与
与 的面积相等,求
的面积相等,求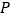 点的坐标.
点的坐标.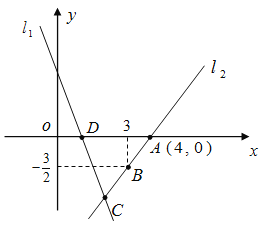
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
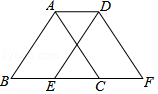
A.11
B.10
C.9
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm.经测量,这条边的实际长度为15m,则这块草坪的实际面积是( )
A. 100m2 B. 270m2 C. 2700m2 D. 90000m2
相关试题

