【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.

参考答案:
【答案】![]() 或写成
或写成 ![]()
【解析】分析:根据三角形中位线定理可求出S1的值,进而可得出S2的值,找出规律即可得出S2018的值.
详解:∵E是BC的中点,ED∥AB,
∴DE是△ABC的中位线,
∴DE=![]() AB,
AB,
∴S△DCE=![]() S△ABC.
S△ABC.
同理,S△BEF=![]() S△ABC.
S△ABC.
∴S1=S△ABC-S△DCE-S△BEF=![]() ×S△ABC,
×S△ABC,
同理求得S2=![]() ×S△ABC,
×S△ABC,
…
S2018=![]() ×S△ABC=
×S△ABC=![]() ×1=
×1=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后OM恰好平分∠BOC,则t= (直接写结果)
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多少秒后OC平分∠MON?请说明理由;
(3)在(2)问的基础上,那么经过多少秒∠MOC=36°?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,
从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.

A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C.
 <MN<
<MN< D.
D.  <MN≤
<MN≤
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了
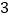 千米到达小彬家,继续走
千米到达小彬家,继续走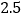 千米到达小颖家,然后向西走了
千米到达小颖家,然后向西走了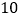 千米到达小明家,最后回到超市.
千米到达小明家,最后回到超市.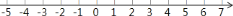
 以超市为原点,以向东的方向为正方向,用
以超市为原点,以向东的方向为正方向,用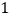 个单位长度表示
个单位长度表示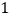 千米,在数轴上表示出小明家,小彬家,小颖家的位置.
千米,在数轴上表示出小明家,小彬家,小颖家的位置.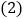 小明家距小彬家多远?
小明家距小彬家多远?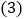 若该货车每千米耗油
若该货车每千米耗油 升,每升油
升,每升油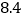 元,那么这辆货车在行驶中一共花费多少油钱?
元,那么这辆货车在行驶中一共花费多少油钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,DE⊥AB于E,DF⊥BC于F.
(1)求证:△ADE≌△CDF;
(2)若∠EDF=50°,求∠BEF的度数.
相关试题

