【题目】已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,
从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.

A. 4 B. 5 C. 6 D. 7
参考答案:
【答案】C
【解析】分析:根据平行四边形的判定来进行选择.①两组对边分别平行的四边形是平行四边形;②两组对角分别平行的四边形是平行四边形;③两组对边分别相等的四边形是平行四边形;④一组对边平行且相等的四边形是平行四边形;⑤对角线互相平分的四边形是平行四边形.
详解:共有6组可能:①②;①③;①④;①⑤;②⑤;④⑤.
选择①与②:∵AB∥CD,
∴∠BAO=∠DCO,∠ABO=∠CDO,
在△AOB与△COD中,
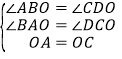 ,
,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD为平行四边形.
①与③(根据一组对边平行且相等)
①与④:∵∠BAD=∠DCB
∴AD∥BC
又AB∥DC
根据两组对边分别平行可推出四边形ABCD为平行四边形.
①与⑤,根据定义,两组对边分别平行的四边形是平行四边形;
②与⑤:∵AD∥BC
OA=OC
∴△AOD≌△COB
故AD=BC,四边形ABCD为平行四边形.
④与⑤:根据两组对边分别平行可推出四边形ABCD为平行四边形.
共有6种可能.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线l1:y=
 (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y= (x﹣2)2+4
(x﹣2)2+4
B.y= (x﹣2)2+3
(x﹣2)2+3
C.y= (x﹣2)2+2
(x﹣2)2+2
D.y= (x﹣2)2+1
(x﹣2)2+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为
 .
.
(1)求口袋中白球的个数;
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后OM恰好平分∠BOC,则t= (直接写结果)
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多少秒后OC平分∠MON?请说明理由;
(3)在(2)问的基础上,那么经过多少秒∠MOC=36°?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )

A. 1<MN<5 B. 1<MN≤5 C.
 <MN<
<MN< D.
D.  <MN≤
<MN≤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车从超市出发,向东走了
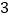 千米到达小彬家,继续走
千米到达小彬家,继续走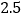 千米到达小颖家,然后向西走了
千米到达小颖家,然后向西走了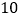 千米到达小明家,最后回到超市.
千米到达小明家,最后回到超市.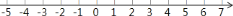
 以超市为原点,以向东的方向为正方向,用
以超市为原点,以向东的方向为正方向,用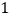 个单位长度表示
个单位长度表示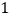 千米,在数轴上表示出小明家,小彬家,小颖家的位置.
千米,在数轴上表示出小明家,小彬家,小颖家的位置.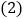 小明家距小彬家多远?
小明家距小彬家多远?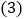 若该货车每千米耗油
若该货车每千米耗油 升,每升油
升,每升油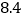 元,那么这辆货车在行驶中一共花费多少油钱?
元,那么这辆货车在行驶中一共花费多少油钱?
相关试题

