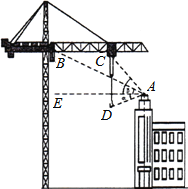
【题目】为了给学生提供更好的学习生活环境,重庆一中寄宿学校2015年对校园进行扩建.某天一台塔吊正对新建教学楼进行封顶施工,工人在楼顶A处测得吊钩D处的俯角α=22°,测得塔吊B,C两点的仰角分别为β=27°,γ=50°,此时B与C距3米,塔吊需向A处吊运材料.(tan27°≈0.5,tan50°≈1.2,tan22°≈0.4)
(1)吊钩需向右、向上分别移动多少米才能将材料送达A处?
(2)封顶工程完毕后需尽快完成新建教学楼的装修工程.如果由甲、乙两个工程队合做,12天可完成;如果由甲、乙两队单独做,甲队比乙队少用10天完成.求甲、乙两工程队单独完成此项工程所需的天数.
参考答案:
【答案】(1)吊钩需向右、向上分别移动![]() 米、
米、![]() 米才能将材料送达A处;(2)甲单独做20天完成此工程,则乙单独做3.天完成此工程.
米才能将材料送达A处;(2)甲单独做20天完成此工程,则乙单独做3.天完成此工程.
【解析】
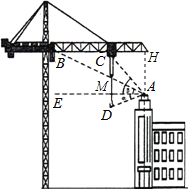
试题分析:(1)过点A作AH⊥BC于点H,则△AHC,△AHB均为Rt△,设CH=x,在△ACH与△ABH中分别用x表示出AH的长,故可得出x的值,进而可得出AM与DM的长,由此得出结论;
(2)设甲单独做y天完成此工程,则乙单独做(y+10)天完成此工程,由甲、乙两个工程队合做,12天可完成求出y的值,进而可得出结论.
解:(1)过点A作AH⊥BC于点H,则△AHC,△AHB均为Rt△,设CH=x,
∵HC∥AE,
∴∠HCA=γ=50°,
∴AH=xtan50°=1.2x.
∵HB∥AE,
∴∠HBA=β=27°,
∴在Rt△ABH中,AH=BHtan27°,即1.2x=(x+3)tan27°,即1.2x=(x+3)![]() ,解得x=
,解得x=![]() .
.
∵四边形AHCM是矩形,
∴AM=![]() .
.
在Rt△AMD中,DM=AMtan22°=![]() ×0.4=
×0.4=![]() .
.
答:吊钩需向右、向上分别移动![]() 米、
米、![]() 米才能将材料送达A处;
米才能将材料送达A处;
(2)设甲单独做y天完成此工程,则乙单独做(y+10)天完成此工程,
由题意得,![]() +
+![]() =
=![]() ,解得y1=20,y2=﹣6(舍去).
,解得y1=20,y2=﹣6(舍去).
经检验,y=20是原分式方程的解且符合题意,
故乙单独完成此项工程的天数为10+20=30(天).
答:甲单独做20天完成此工程,则乙单独做3.天完成此工程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是直角三角形,∠ACB=90°.
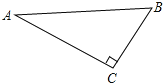
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.
(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求
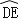 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若正比例函数y=(2-m)x的函数值y随x的增大而减小,则m的取值范围是( )
A. m<0 B. m>0 C. m<2 D. m>2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b,当-3≤x≤1时,对应的函数值的取值范围为1≤y≤9,求k+b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=2是关于x的方程3x+a=0的一个解,则a的值是( )
A. ﹣6 B. ﹣3 C. ﹣4 D. ﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,点E,F在对角线BD上,且BE=DF,求证:
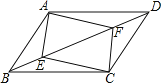
(1)AE=CF;
(2)四边形AECF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张方桌由1个桌面、4条腿组成,如果1立方米木料可以做方桌的桌面50个或桌腿300条,现有5立方米木料,如何分配木料,使做出的桌面和桌腿恰好配成方桌?能配多少方桌?
相关试题

