【题目】如图,某中学为合理安排体育活动,在全校喜欢乒乓球、排球、羽毛球、足球、篮球五种球类运动的1000名学生中,随机抽取了若干名学生进行调查,了解学生最喜欢的一种球类运动,每人只能在这五种球类运动中选择一种.调查结果统计如下:
球类名称 | 乒乓球 | 排球 | 羽毛球 | 足球 | 篮球 |
人数 | a | 12 | 36 | 18 | b |

解答下列问题:
(1)本次调查中的样本容量是;
(2)a= , b=;
(3)试估计上述1000名学生中最喜欢羽毛球运动的人数.
参考答案:
【答案】
(1)120
(2)30;24
(3)解:喜欢羽毛球的人数为:1000× ![]() =300人
=300人
【解析】解:(1)∵喜欢排球的有12人,占10%, ∴样本容量为12÷10%=120;
2)a=120×25%=30人,
b=120﹣30﹣12﹣36﹣18=24人;
【考点精析】通过灵活运用统计表和扇形统计图,掌握制作统计表的步骤:(1)收集整理数据.(2)确定统计表的格式和栏目数量,根据纸张大小制成表格.(3)填写栏目、各项目名称及数据.(4)计算总计和合计并填入表中,一般总计放在横栏最左格,合计放在竖栏最上格.(5)写好表格名称并标明制表时间;能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣
 x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(π﹣5)0+ ﹣|﹣3|
﹣|﹣3|
(2)3a+(1+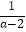 )
)  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.

(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数的概率.(请用“画树状图”或“列表”的方法写出过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.

(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD= ,求⊙O的半径.
,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.

(1)求小亮从乙地到甲地过程中y2(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
相关试题

