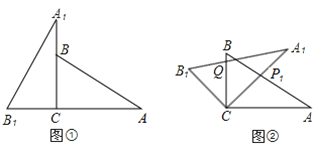
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
参考答案:
【答案】(1)证明见解析;(2)CQ=![]()
【解析】(1)利用△A1CB1≌△ACB得到CA1=CA,再根据旋转的性质得∠B1CB=∠A1CA=45°,则∠BCA1=45°,于是根据“ASA”判断△CQA1≌△CP1A,所以CP1=CQ;
(2)过点P1作P1P⊥AC于点P,如图②,先在Rt△AP1P中根据含30度的直角三角形三边的关系得到P1P=![]() AP1=
AP1=![]() ×2=1,然后在Rt△CP1P中利用等腰直角三角形的性质得CP=P1P=1,CP1=
×2=1,然后在Rt△CP1P中利用等腰直角三角形的性质得CP=P1P=1,CP1=![]() PP1=
PP1=![]() ,由(1)得CQ=CP1=
,由(1)得CQ=CP1=![]() .
.
(1)∵△A1CB1≌△ACB,∴CA1=CA.
∵图①中的△A1B1C顺时针旋转45°得图②,∴∠B1CB=∠A1CA=45°,∴∠BCA1=45°.
在△CQA1和△CP1A中,∵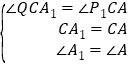 ,∴△CQA1≌△CP1A,∴CP1=CQ;
,∴△CQA1≌△CP1A,∴CP1=CQ;
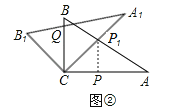
(2)过点P1作P1P⊥AC于点P,如图②.在Rt△AP1P中,∵∠A=30°,∴P1P=![]() AP1=
AP1=![]() ×2=1.在Rt△CP1P中,∵∠P1CP=45°,∴CP=P1P=1,∴CP1=
×2=1.在Rt△CP1P中,∵∠P1CP=45°,∴CP=P1P=1,∴CP1=![]() PP1=
PP1=![]() ,∴CQ=CP1=
,∴CQ=CP1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
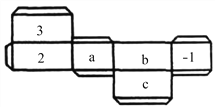
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)+4abc].
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab<0,则正比例函数y=ax与反比例函数
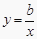 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
A.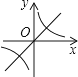
B.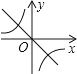
C.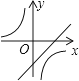
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
 是反比例函数,且图象在第一,三象限,那么m的值是( )
是反比例函数,且图象在第一,三象限,那么m的值是( )
A.±1
B.1
C.-1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明用三个等腰三角形(图中①②③)拼成了一个平行四边形ABCD,且
 ,则
,则 =_____ 度.
=_____ 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
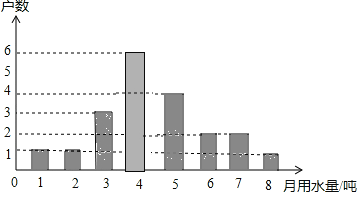
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
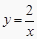 ,下列结论中,不正确的是( )
,下列结论中,不正确的是( )
A.图象必经过点(1,2)
B.y随x的增大而增大
C.图象在第一、三象限内
D.若x>1,则0<y<2
相关试题

