【题目】已知直线y=![]() x+3与两坐标轴分别相交于A、B两点,若点P、Q分别是线段AB、OB上的动点,且点P不与A、B重合,点Q不与O、B重合.
x+3与两坐标轴分别相交于A、B两点,若点P、Q分别是线段AB、OB上的动点,且点P不与A、B重合,点Q不与O、B重合.
(1)若OP⊥AB于点P,△OPQ为等腰三角形,这时满足条件的点Q有几个?请直接写出相应的OQ的长;
(2)当点P是AB的中点时,若△OPQ与△ABO相似,这时满足条件的点Q有几个?请分别求出相应的OQ的长;
(3)试探究是否存在以点P为直角顶点的Rt△OPQ?若存在,求出相应的OQ的范围,并求出OQ取最小值时点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1) 点Q有三个,OQ的长为2或![]() 或
或![]() ;(2) 2个,OQ的长为2或
;(2) 2个,OQ的长为2或![]() ;(3)存在,OQ取最小值时点P的坐标(
;(3)存在,OQ取最小值时点P的坐标(![]() ,
,![]() ).
).
【解析】
试题分析:(1)如图1中,满足条件的点Q有三个,分三种情形讨论即可①QO=QP,②OP=OQ,③PO=PQ.
(2)如图2中,满足条件的点Q有2个.作![]() ⊥OB于
⊥OB于![]() ,
,![]() ⊥OP于
⊥OP于![]() ,可以证明
,可以证明![]() 、
、![]() 满足条件,理由相似三角形的性质即可解决问题.
满足条件,理由相似三角形的性质即可解决问题.
(3)存在.以OQ为直径作⊙G,当⊙G与AB相切于点P时,∠OPQ=90°,此时OQ的值最小.由此求出OQ,即可解决问题.
试题解析:(1)如图1中,满足条件的点Q有三个.
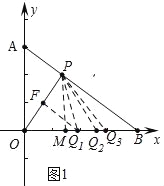
理由:作PM⊥OB于M,作OP的垂直平分线交OP于F,交OB于![]() .则
.则![]() =
=![]() ,△
,△![]() 是等腰三角形,此时
是等腰三角形,此时![]() =
=![]() OB=2.
OB=2.
∵A(0,3),B(4,0),
∴OA=3,OB=4,AB=5,
∵OP⊥AB,
∴![]() OAOB=
OAOB=![]() ABOP,
ABOP,
∴OP=![]() =
=![]() ,
,
当![]() =OP时,△
=OP时,△![]() 是等腰三角形,此时
是等腰三角形,此时![]() =
=![]() ,
,
当PO=![]() 时,∵PM⊥
时,∵PM⊥![]() ,
,
∴![]() =2OM,
=2OM,
∵∠POM=∠![]() ,∠PMO=∠OPB,
,∠PMO=∠OPB,
∴△OPM∽△OBP,
∴![]() =OMOB,
=OMOB,
∴OM=![]() ,
,
∴![]() =
=![]() .
.
综上所述,△OPQ为等腰三角形时,满足条件的点Q有三个,OQ的长为2或![]() 或
或![]() .
.
(2)如图2中,满足条件的点Q有2个.
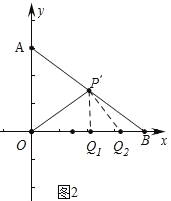
理由:作![]() ⊥OB于
⊥OB于![]() ,
,![]() ⊥OP于
⊥OP于![]() ,
,
∵PA=PB,∠AOB=90°,
∴PA=PB=PO,
∴∠![]() =∠ABO,∵∠
=∠ABO,∵∠![]() =∠AOB,
=∠AOB,
∴△![]() ∽△BAO,
∽△BAO,
∵PA=PB,![]() ∥OA,
∥OA,
∴![]() =
=![]() =
=![]() OB=2,
OB=2,
∵∠![]() =∠ABO,∠
=∠ABO,∠![]() =∠AOB,
=∠AOB,
∴△![]() ∽△BOA,
∽△BOA,
∴![]() ,
,
∴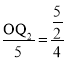 ,
,
∴![]() =
=![]() ,
,
综上所述,△OPQ与△ABO相似时,满足条件的点Q有2个,OQ的长为2或![]() .
.
(3)存在.理由如下:
如图3中,以OQ为直径作⊙G,当⊙G与AB相切于点P时,∠OPQ=90°,此时OQ的值最小.
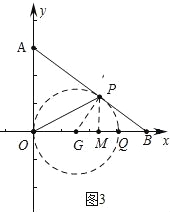
∴设OG=GP=r,
∵AO=AP=3,
∴PB=AB=AP=2,
在Rt△PBG中,∵∠GPB=90°,PG=r,BG=4﹣r,PB=2,
∴![]() ,
,
∴r=![]() ,
,
∴OQ=2r=3,
∴当3≤OQ<4时,△OPQ可为直角三角形.
作PM⊥OB于M.
∵PM∥OA,
∴![]() ,
,
∴![]() ,
,
∴PM=![]() ,BM=
,BM=![]() ,
,
∴OM=4﹣![]() =
=![]() ,
,
∴OQ取最小值时点P的坐标(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的三边长的平方和为200,则斜边长为________
-
科目: 来源: 题型:
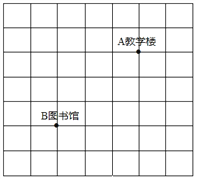
查看答案和解析>>【题目】如图为东明一中新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的位置坐标为B(-2,-1),解答以下问题:
(1)在图中找到坐标系中的原点,并建立直角坐标系;
(2)若体育馆的坐标为C(1,-3),食堂坐标为D(2,0),请在图中标出体育馆和食堂的位置;
(3)顺次连接教学楼、图书馆、体育馆、食堂得到四边形ABCD,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是﹣2.
已知点A是数轴上的点,完成下列各题:
(1)如果点A表示的数是3,将点A先向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是 , A、B两点间的距离为;
(2)如果点A表示的数是﹣4,将点A先向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是 , A、B两点间的距离为;
一般地,如果点A表示的数是m,将点A先向右移动n个单位长度,再向左移动t个单位长度,那么终点B表示的数是 , A、B两点间的距离为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】希望工程义演出售两种票,成人票每张10元,儿童票每张6元,共卖出1000张票,如果成人票卖了x张,出售儿童票共收入钱数为( )
A.(1000﹣x)元
B.6(1000﹣x)元
C.6x元
D.10(1000﹣x)元 -
科目: 来源: 题型:
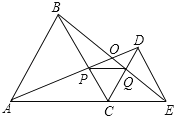
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三边之比为5∶12∶13,它的周长为60,则它的面积是________.
相关试题

