【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与y轴的正半轴交于点A,与x轴交于点
的图象与y轴的正半轴交于点A,与x轴交于点![]() ,
,![]() 的面积为
的面积为![]() 动点P从点B出发,以每秒1个单位长度的速度在射线BO上运动,动点Q从O出发,沿x轴的正半轴与点P同时以相同的速度运动,过P作
动点P从点B出发,以每秒1个单位长度的速度在射线BO上运动,动点Q从O出发,沿x轴的正半轴与点P同时以相同的速度运动,过P作![]() 轴交直线AB于M.
轴交直线AB于M.
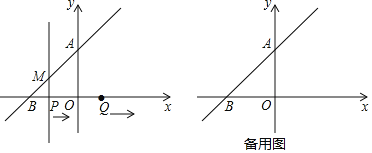
![]() 求直线AB的解析式.
求直线AB的解析式.
![]() 当点P在线段OB上运动时,设
当点P在线段OB上运动时,设![]() 的面积为S,点P运动的时间为t秒,求S与t的函数关系式
的面积为S,点P运动的时间为t秒,求S与t的函数关系式![]() 直接写出自变量的取值范围
直接写出自变量的取值范围![]() .
.
![]() 过点Q作
过点Q作![]() 轴交直线AB于N,在运动过程中
轴交直线AB于N,在运动过程中![]() 不与B重合
不与B重合![]() ,是否存在某一时刻
,是否存在某一时刻![]() 秒
秒![]() ,使
,使![]() 是等腰三角形?若存在,求出时间t值.
是等腰三角形?若存在,求出时间t值.
参考答案:
【答案】(1)y=x+2;(2)S=t(0<t≤2);(3)存在,t=2或2![]() ﹣2.
﹣2.
【解析】
(1)S△ABO=![]() ×OA×OB=
×OA×OB=![]() ×AO×2=2,则OA=2,即点A(0,2),即可求解;
×AO×2=2,则OA=2,即点A(0,2),即可求解;
(2)t秒时,点P的坐标为(-2+t,0),则MP=BP=t,S=![]() ×PQ×MP,即可求解;
×PQ×MP,即可求解;
(3)分MN=MQ、MN=NQ、MQ=NQ三种情况,求解即可.
(1)S△ABO=![]() ×OA×OB=
×OA×OB=![]() ×AO×2=2,则OA=2,即点A(0,2),
×AO×2=2,则OA=2,即点A(0,2),
将点A、B的坐标代入一次函数表达式:y=km+n,得:![]() ,
,
解得:![]() ,
,
故直线AB的表达式为:y=x+2;
(2)t秒时,点P的坐标为(﹣2+t,0),则MP=BP=t,
S=![]() ×PQ×MP=
×PQ×MP=![]() ×2t=t(0<t≤2);
×2t=t(0<t≤2);
(3)存在,理由:
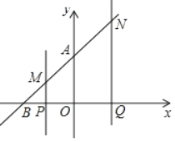
t秒时,点M、N、Q的坐标分别为(﹣2+t,t)、(t,t+2)、(t,0),
则:MN2=4+4=8,MQ2=4+t2,NQ2=(t+2)2,
当MN=MQ时,即:8=4+t2,t=2(负值已舍去),
当MN=NQ时,同理可得:t=2![]() ﹣2(负值已舍去),
﹣2(负值已舍去),
当MQ=NQ时,同理可得:t=0(舍去),
故:当△MNQ是等腰三角形时,t=2或2![]() ﹣2.
﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果
芦柑
香梨
每辆汽车载货量
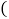 吨
吨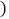
7
6
5
每车水果获利
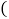 元
元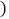
2500
3000
2000
 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】初二
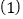 班同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行
班同学从学校出发去某自然保护区研学旅行,一部分乘坐大客车先出发,余下的几人20分钟后乘坐小轿车沿同一路线出行 大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的
大客车中途停车等候,小轿车赶上来之后,大客车以出发时速度的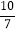 继续行驶,小轿车保持原速度不变
继续行驶,小轿车保持原速度不变 小轿车司机因路线不熟错过了景点入口,再原路提速返回,恰好与大客车同时到达景点入口
小轿车司机因路线不熟错过了景点入口,再原路提速返回,恰好与大客车同时到达景点入口 两车距学校的路程
两车距学校的路程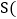 单位:千米
单位:千米 和行驶时间
和行驶时间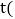 单位:分钟
单位:分钟 之间的函数关系如图所示.
之间的函数关系如图所示.请结合图象解决下面问题:
 学校到景点的路程为______千米,大客车途中停留了______分钟,
学校到景点的路程为______千米,大客车途中停留了______分钟, ______千米;
______千米; 在小轿车司机驶过景点入口时,大客车离景点入口还有多远?
在小轿车司机驶过景点入口时,大客车离景点入口还有多远? 若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待______分钟,大客车才能到达景点入口.
若大客车一直以出发时的速度行驶,中途不再停车,那么小轿车折返后到达景点入口,需等待______分钟,大客车才能到达景点入口.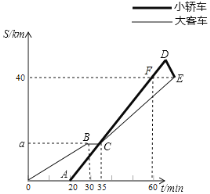
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家距离学校8千米,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?(结果精确到0.1)

-
科目: 来源: 题型:
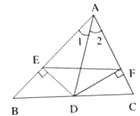
查看答案和解析>>【题目】已知,如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高。求证:AD垂直平分EF。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
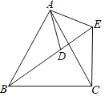
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB=CB,F为AB延长线上一点,点E在BC上,且AE=CF,若∠CAE=32°,则∠ACF的度数为__________°.

相关试题

