【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
(1)判断MN与AC的位置关系;
(2)求点D由点A向点B匀速运动的过程中,线段MN所扫过区域的面积;
(3)若△DMN是等腰三角形,求t的值.

参考答案:
【答案】(1)MN∥AC;
(2)线段MN所扫过区域的面积为12;
(3)当t=5或6或![]() 时,△DMN为等腰三角形.
时,△DMN为等腰三角形.
【解析】
试题分析:(1)利用三角形中位线证明即可;
(2)分别取△ABC三边AC,AB,BC的中点E,F,G,并连接EG,FG,根据题意可得线段MN扫过区域的面积就是AFGE的面积求解即可;
(3)分三种情况:①当MD=MN=3时,②当MD=DN,③当DN=MN时,分别求解△DMN为等腰三角形即可.
试题解析:(1)∵在△ADC中,M是AD的中点,N是DC的中点,
∴MN∥AC;
(2)如图1,分别取△ABC三边AC,AB,BC的中点E,F,G,并连接EG,FG,
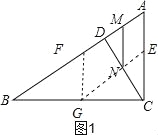
根据题意可得线段MN扫过区域的面积就是AFGE的面积,
∵AC=6,BC=8,
∴AE=3,GC=4,
∵∠ACB=90°,
∴S四边形AFGE=AEGC=3×4=12,
∴线段MN所扫过区域的面积为12.
(3)据题意可知:MD=![]() AD,DN=
AD,DN=![]() DC,MN=
DC,MN=![]() AC=3,
AC=3,
①当MD=MN=3时,△DMN为等腰三角形,此时AD=AC=6,
∴t=6,
②当MD=DN时,AD=DC,如图2,过点D作DH⊥AC交AC于H,则AH=![]() AC=3,
AC=3,
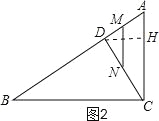
∵cosA=![]() ,
,
∴![]() ,解得AD=5,
,解得AD=5,
∴AD=t=5.
③如图3,当DN=MN=3时,AC=DC,连接MC,则CM⊥AD,
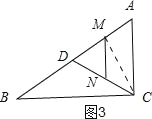
∵cosA=![]() ,即
,即![]() ,
,
∴AM=![]() ,
,
∴AD=t=2AM=![]() ,
,
综上所述,当t=5或6或![]() 时,△DMN为等腰三角形.
时,△DMN为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果不等式组
 有解.那么m的取值范围是( )
有解.那么m的取值范围是( )
A.m>8
B.m≥8
C.m<8
D.m≤8 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:16m3﹣mn2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上所表示的是哪一个不等式的解集 ( )

A. x>-1
x>-1
B. ≥-3
≥-3
C.x+1≥-1
D.-2x>4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,在△ABC中,D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)求∠AFC的度数;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有限小数和无限循环小数统称数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
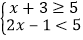 的解集在数轴上表示为
的解集在数轴上表示为
A.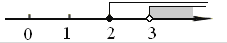
B.
C.
D.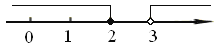
相关试题

