Question

【题目】完成下面推理过程

如图，已知DE∥BC，DF、BE分别平分∠ADE、∠ABC，可推得∠FDE=∠DEB的理由：

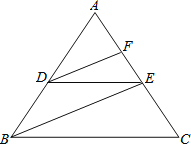
∵DE∥BC（已知）

∴∠ADE=　　　　　　．（　　　　　 　 ）

∵DF、BE分别平分∠ADE、∠ABC，

∴∠ADF=　　　　　　，

∠ABE=　　　　　　．（　　　　　 　）

∴∠ADF=∠ABE

∴DF∥　 　　．（　　　　　 　）

∴∠FDE=∠DEB． （　　　　　　 ）

Answer 1

【答案】∠ABC 两直线平行，同位角相等 ∠ADE ∠ABC 角平分线的定义 BE 同位角相等，两直线平行 两直线平行，内错角相等

【解析】试题分析：根据平行线的性质由DE∥BC得∠ADE=∠ABC，再根据角平分线的定义得到∠ADF=∠ADE，∠ABE=∠ABC，则∠ADF=∠ABE，然后根据平行线的判定得到DF∥BE，最后利用平行线的性质得∠FDE=∠DEB．

试题解析：解：∵DE∥BC，（已知）

∴∠ADE=∠ABC，（两直线平行，同位角相等）

∵DF、BE分别平分∠ADE、∠ABC，

∴∠ADF=∠ADE，

∠ABE=∠ABC，（角平分线的定义）

∴∠ADF=∠ABE，

∴DF∥BE，（同位角相等，两直线平行．）

∴∠FDE=∠DEB．（两直线平行，内错角相等）