【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,求∠MNA的度数.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长;

参考答案:
【答案】(1)50°;(2)6 cm.
【解析】试题分析:
(1)由AB=AC可得∠C=∠ABC=70°,从而可得∠A=40°;由MN垂直平分AB可得AN=BN,可得∠ABN=∠A=40°,从而可得∠ANB=100°,再由等腰三角形的三线合一可得∠MNA=![]() ∠ANB=50°;
∠ANB=50°;
(2)由(1)可知BN=AN,由此可得BN+NC=AN+NC=AC=AB=8cm,再由C△BNC=BN+CN+BC=14cm,可得BC=14-8=6(cm).
试题解析:
(1)∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠A=40°,
∵MN是AB的垂直平分线,
∴AN=BN,
∴∠ABN=∠A=40°,
∴∠ANB=100°,
∴∠MNA=50°.
(2)由(1)可知:AN=BN,
∴BN+CN=AN+CN=AC,
∵AB=AC=8cm,
∴BN+CN=8cm,
∵C△BNC=BN+CN+BC=14(cm),
∴BC=14﹣8=6(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(a3)2=a5
B.a2a3=a5
C.a6÷a2=a3
D.3a2﹣2a2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】有一道题目是一个多项式加上多项式xy﹣3yz﹣2xz,某同学以为是减去这个多项式,因此计算得到的结果为2xy﹣3yz+4xz.请你改正他的错误,求出正确的答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果高出海平面20米,记作+20米,那么﹣30米表示( )
A.不足30米
B.低于海平面30米
C.高出海平面30米
D.低于海平面20米 -
科目: 来源: 题型:
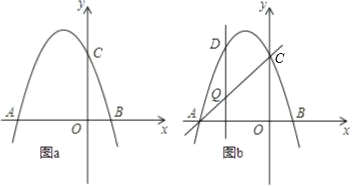
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果钟面上的时间是8:30,则分针与时针的夹角是_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a﹣2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
相关试题

