【题目】已知y=y ![]() +y
+y ![]() ,y
,y ![]() 与x
与x ![]() 成正比例,y
成正比例,y ![]() 与x-1成反比例,并且x=0时y=1,x=-1时y=2;求当x=2时y的值.
与x-1成反比例,并且x=0时y=1,x=-1时y=2;求当x=2时y的值.
参考答案:
【答案】解: ![]()
![]() 与
与 ![]() 成正比例,可设
成正比例,可设 ![]() ,
, ![]() 与x-1成反比例,可设
与x-1成反比例,可设 ![]()
![]()
![]() ,又
,又 ![]() x=0,y=1 x=-1,y=2
x=0,y=1 x=-1,y=2
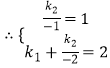 解得
解得 ![]() ,
, ![]()
解析式为 ![]() ,把x=2代入,解得y=5
,把x=2代入,解得y=5
【解析】先根据题意分别表示出y 1 与 x 2 和 y 2 与x-1的函数解析式,注意两函数的系数不能用同一个字母表示,再将y 1 ,y 2 代入y=y 1 +y 2 表示出y与x的函数解析式,然后将x、y的两组值代入,建立方程组求解,可得出函数解析式,再将x=2的值代入即可求出函数值。
【考点精析】掌握解二元一次方程组和一次函数的概念是解答本题的根本,需要知道二元一次方程组:①代入消元法;②加减消元法;一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

-
科目: 来源: 题型:
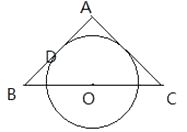
查看答案和解析>>【题目】如图所示,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于D点. 求证:AC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD、BE分别是钝角三角形ABC的边BC、AC上的高.

求证: =
= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外圴相同.
(1)从箱子里任意摸出一个球是白球的概率是多少?
(2)从箱子里任意摸出一个球,不将它放回,搅均后再摸出一球,求两次摸出的球都是白球的概率,并画出树状图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若∠B=∠ACB,CE=5,CF=7,求DB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系内,点
 为坐标原点,点
为坐标原点,点 在
在 轴正半轴上,点
轴正半轴上,点 在
在 轴的负半轴上,点
轴的负半轴上,点 在
在 轴正半轴上,
轴正半轴上, ,梯形
,梯形 的面积为
的面积为 ,
, ,
, .
.(1)求点
 ,
, 的坐标;
的坐标;(2)点
 从点
从点 出发以
出发以 个单位/秒的速度沿
个单位/秒的速度沿 向终点
向终点 运动,同时,点
运动,同时,点 从点
从点 出发以
出发以 个单位秒的速度沿
个单位秒的速度沿 向终点
向终点 运动,设点
运动,设点 的横坐标为
的横坐标为 ,线段
,线段 的长为
的长为 ,用含
,用含 的关系式表示
的关系式表示 ,并直接写出相应的
,并直接写出相应的 范围.
范围.
相关试题

