【题目】如图,在平面直角坐标系内,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发以
出发以![]() 个单位/秒的速度沿
个单位/秒的速度沿![]() 向终点
向终点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发以
出发以![]() 个单位秒的速度沿
个单位秒的速度沿![]() 向终点
向终点![]() 运动,设点
运动,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,用含
,用含![]() 的关系式表示
的关系式表示![]() ,并直接写出相应的
,并直接写出相应的![]() 范围.
范围.

参考答案:
【答案】(1)![]() ,
,![]() ,(2)当
,(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)设AO为x,则BO=AD=x,OC=2x,根据梯形的面积公式列出方程,即可求出x的值,再得出B,C的坐标即可;
(2)根据题意设t秒后P在数轴上表示的数为8-3t,则Q点为-4+t,再根据P、Q相遇前与相遇后分别进行讨论即可.
解:(1)设AO为x,则BO=AD=x,OC=2x,
依题意得![]()
解得x=4,(x=-4舍去)
∴![]() ,
,![]() .
.
(2)设t秒后P在数轴上表示的数为8-3t,则Q点为-4+t,
①P、Q相遇前:
即![]() 时,d=PQ=(8-3t)-( -4+t)=12-4t,
时,d=PQ=(8-3t)-( -4+t)=12-4t,
又m=8-3t,
∴![]() ;
;
②P、Q相遇后,即当![]() 时,且P,Q分别在B,C处停下,
时,且P,Q分别在B,C处停下,
d=PQ=( -4+t)-(8-3t) =-12+4t,
m=8-3t,
∴![]() .
.
故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y
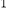 +y
+y 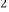 ,y
,y 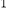 与x
与x 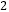 成正比例,y
成正比例,y 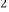 与x-1成反比例,并且x=0时y=1,x=-1时y=2;求当x=2时y的值.
与x-1成反比例,并且x=0时y=1,x=-1时y=2;求当x=2时y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外圴相同.
(1)从箱子里任意摸出一个球是白球的概率是多少?
(2)从箱子里任意摸出一个球,不将它放回,搅均后再摸出一球,求两次摸出的球都是白球的概率,并画出树状图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.
(1)证明:△ADE≌△CFE;
(2)若∠B=∠ACB,CE=5,CF=7,求DB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC三条边的长度分别是
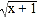 ,
, ,
, ,记△ABC的周长为C△ABC.
,记△ABC的周长为C△ABC.(1)当x=2时,△ABC的最长边的长度是 (请直接写出答案);
(2)请求出C△ABC(用含x的代数式表示,结果要求化简);
(3)我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=
 .其中三角形边长分别为a,b,c,三角形的面积为S.
.其中三角形边长分别为a,b,c,三角形的面积为S.若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售一种销售成本为40元/千克的水产品,若 50元 /千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.
(1)写出月销售利润y(单位:元) 与售价x(单位:元/千克) 之间的函数解析式.
(2)当售价定为多少时会获得最大利润?求出最大利润.
(3)商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元销售单价应定为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠COE=90°,OF平分∠AOE.
(1)若∠COF=40°,求∠BOE的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE=______(用含α的式子表示).

相关试题

