【题目】如图,在平面直角坐标系中,直线y1=2x2与坐标轴交于A、B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )

A. 当x>0时,y1随x的增大而增大,y2随x的增大而减小;
B. k=4
C. 当0<x<2时,y1<y2
D. 当x=4时,EF=4
参考答案:
【答案】D
【解析】试题分析:A、从图象可知:当x>0时,y1随x的增大而增大,y2随x的增大而减小,故本选项不符合题意;
B、y1=2x-2,
当y=0时,x=1,
即OA=1,
∵OA=AD,
∴OD=2,
把x=2代入y=2x-2得:y=2,
即点C的坐标是(2,2),
把C的坐标代入双曲线y2=![]() (x>0)得:k=4,故本选项不符合题意;
(x>0)得:k=4,故本选项不符合题意;
C、根据图象可知:当0<x<2时,y1<y2,故本选项不符合题意;
D、当x=4时,y1=2×4-2=6,y2=![]() =1,
=1,
所以EF=6-1=5,故本选项符合题意.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次团体操排练活动中,

(1)如图,老师让大家站成一个形如正方形的点阵,第一层每边有三个点,第二层每边有五个点,第三层每边有七个点,依此类推,则第四层的总点数是 ;第n层(n为正整数)的总点数是 ;
(2)某班45名学生面向老师站成一列横队.老师每次让其中任意6名学生向后转(不论原来方向如何),能否经过若干次后全体学生都背向老师站立?如果能够,请你设计一种方案;如果不能够,请联系有理数乘法的知识说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC中,D为边AC上一点.
(1)以BD为边作等边△BDE,连接CE,求证:AD=CE;
(2)如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=
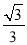 x2+
x2+ x﹣
x﹣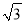 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y=
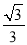 x2+
x2+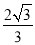 x﹣
x﹣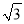 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由. 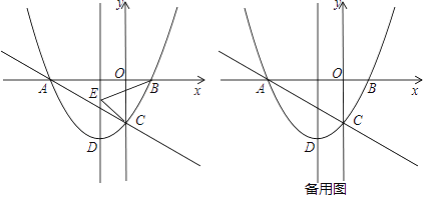
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的
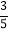 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=a.作BC边的三等分点C1,使得CC1∶BC1=1∶2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2∶BC2=1∶2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为( )

A.
 aB.
aB.  aC.
aC.  aD.
aD.  a
a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3
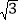 .其中正确的结论有( )
.其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
相关试题

