Question

【题目】在中，.

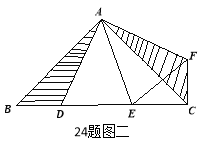
（1）如图1，若点关于直线的对称点为，求证：∽；

（2）如图2，在（1）的条件下，若，求证：；

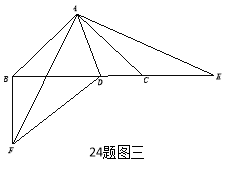
（3）如图3，若，点在的延长线上，则等式还能成立吗？请说明理由.

Answer 1

【答案】(1)详见解析；（2）详见解析；（3）成立，理由见解析.

【解析】

试题分析：（1）根据已知易证，，再由AB=AC，根据两边的比相等夹角相等，两三角形全相似，即可得∽；（2）先证≌，可得和，即可判定，由勾股定理及等量代换可得结论；（3）将顺时针旋转，得，易证，根据勾股定理可得，再证≌，可得，所以.

试题解析：（1）关于直线对称①

∽

（2）

即

又≌②

和

即

在中，，结合已证明的①②得，所以

（3）解法一：将顺时针旋转，得.

③和

即④

由旋转的性质，

,

已证明，边公共

≌即⑤.将③⑤代入④式，

得

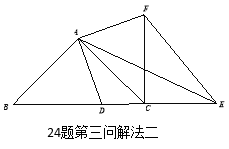
解法二：作关于直线对称⑥

即

,

≌⑦和

因此

所以将⑥⑦代入得

考点:三角形综合题.