【题目】如图,一次函数y1=x+m(m>0)的图象与x轴交于点A,一次函数y2=nx+2的图象与x轴交于点B,点P( ![]() )是两函数图象的交点.
)是两函数图象的交点.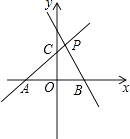
(1)求函数y1、y2的关系式;
(2)若∠PBA=64°,求∠APB的度数;
(3)求四边形PCOB的面积;
(4)在x轴上,是否存在一点Q,使以点Q、B、C为顶点的三角形是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵P( ![]() )是两函数图象的交点,
)是两函数图象的交点,
∴ ![]()
解得:m=1,n=﹣2,
所以y1=x+1,y2=﹣2x+2;
(2)解:把x=0代入y1=x+1,可得y=1,
把y=0代入y1=x+1,可得x=﹣1,
所以OA=OC=1,
所以∠CAB=45°,
∵∠PBA=64°,
∴∠APB=180°﹣45°﹣64°=71°;
(3)解:∵直线y1=x+1与x,y轴分别交于点A,C,
∴A(﹣1,0),C(0,1),
∴OA=1,OC=1,
∵直线y2=﹣2x+2与x轴交于点B,
∴B(1,0),
∴OB=1,
∴AB=|1﹣(﹣1)|=2,
∴ 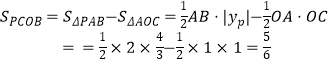 ;
;
(4)解:①当QB=QC时,Q(0,0);
②当BQ=BC时,点Q( ![]() ,0)或(
,0)或( ![]() ,0);
,0);
③当BC=QC时,Q(﹣1,0).
【解析】(1)由“点P 是两函数图象的交点”可把P坐标分别代入两解析式中,可求出函数y1、y2的关系式;(2)一次函数y1=x+m的k值为1,可放在RtΔAOC中由OA=OC,求出∠CAB=45°,进而由内角和求出∠APB的度数;(3)不规则四边形面积通常可采用作差法或求和法,本题的S四边形PCOB=SΔPABSΔAOC;(4)出现等腰三角形时,若没指明腰和底,需分类讨论,分别以三个顶点为顶角顶点进行分类,根据等腰三角形的性质得出Q坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+x﹣1的值为0,则代数式x3+2x2+2007的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:6cos45°+(
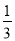 )﹣1+(
)﹣1+(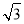 ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3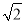 |+42017×(﹣0.25)2017
|+42017×(﹣0.25)2017(2)先化简,再求值:(
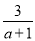 ﹣a+1)÷
﹣a+1)÷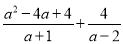 ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
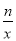 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.(1)求一次函数与反比例函数的解析式;
(2)直接写出当x>0时,kx+b﹣
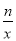 <0的解集.
<0的解集.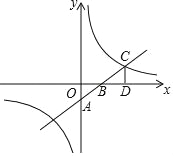
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用全面调查(普查)的是( )
A.某班学生对国家“一带一路”战略的知晓率
B.鞋厂检测生产的鞋底能承受的弯曲次数
C.检测某城市的空气质量
D.了解电视栏目《朗读者》的收视率
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:aa2+a5÷a2﹣3a3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由多项式乘法:(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式:x2+(a+b)x+ab=(x+a)(x+b)
示例:分解因式:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3)
(1)尝试:分解因式:x2+6x+8=(x+)(x+);
(2)应用:请用上述方法解方程:x2﹣3x﹣4=0.
相关试题

