【题目】如图(1),直线![]() ⊥
⊥![]() 轴于点P,Rt△ABC中,斜边AB=5,直角边AC=3,点A(0,
轴于点P,Rt△ABC中,斜边AB=5,直角边AC=3,点A(0, ![]() )在
)在![]() 轴上运动,直角边BC在直线
轴上运动,直角边BC在直线![]() 上,将△ABC绕点P顺时针旋转90°,得到△DEF。以直线
上,将△ABC绕点P顺时针旋转90°,得到△DEF。以直线![]() 为对称轴的抛物线经过点F。
为对称轴的抛物线经过点F。
(1)求点F的坐标(用含![]() 的式子表示)
的式子表示)
(2)①如图(2)当抛物线的顶点为点C时,抛物线恰好过坐标原点。求此时抛物线的解析式;
②如图(3)不改变①中抛物线的开口方向和形状,让点A的位置发生变化,使抛物线与线段AB始终有交点M(![]() ,
, ![]() ).
).
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)变化过程中,当![]() 变成某一个值时,点A的位置唯一确定,求此时点M的坐标。
变成某一个值时,点A的位置唯一确定,求此时点M的坐标。



图(1) 图(2) 图(3)
参考答案:
【答案】(1)点F的坐标为(![]() ,0);(2)①
,0);(2)①![]() ;②(ⅰ)
;②(ⅰ) ![]() ;(ii)点M的坐标为(
;(ii)点M的坐标为(![]() ,
, ![]() )
)
【解析】(1)由旋转可知,PF=PC=|t |,当![]() t
t![]() 时,OF=OP+PF=t+3
时,OF=OP+PF=t+3![]() ,易知F(t+3
,易知F(t+3![]() ,0);
,0);
当![]() 时,OF=OP-PF=
时,OF=OP-PF= ![]() ,点F坐标为(
,点F坐标为(![]() ,0); 当
,0); 当![]() 时,OF= PF-OP=
时,OF= PF-OP=![]() ,点F坐标仍为点F坐标为(
,点F坐标仍为点F坐标为(![]() ,0)
,0)
∴点F的坐标为(![]() ,0)
,0)
(2)①由抛物线的对称性可知,PF=PO=3,又由旋转PC=PF,故此时点C坐标为(3,3),设抛物线的解析式为![]() ,将原点坐标代入可得:
,将原点坐标代入可得: ![]()
∴此时抛物线的解析式为![]()
②由于抛物线形状和对称轴不发生改变,故可设抛物线解析式为![]() ,由于抛物线过点F(
,由于抛物线过点F(![]() ,0),代入可得:
,0),代入可得: ![]() ,即此时抛物线为
,即此时抛物线为![]()
(ⅰ)易求点B坐标为(3, ![]() ),由于
),由于![]() ,∴点B恒在抛物线顶点下方,只有点A在抛物线上或上方,抛物线与线段AB才有交点。
,∴点B恒在抛物线顶点下方,只有点A在抛物线上或上方,抛物线与线段AB才有交点。
当![]() 从0开始增大时,PF增大,抛物线与
从0开始增大时,PF增大,抛物线与![]() 轴左边交点向左移动,抛物线与
轴左边交点向左移动,抛物线与![]() 轴交点随之上移,点M逐渐向点A靠拢,当抛物线过点A时,
轴交点随之上移,点M逐渐向点A靠拢,当抛物线过点A时, ![]() 取得最大值;而当
取得最大值;而当![]() 从0开始减小时点F在O、P之间,由于抛物线随着
从0开始减小时点F在O、P之间,由于抛物线随着![]() 的减小向上移动,而点A向下移动,故点M会向点A靠拢,故当抛物线经过点A时,
的减小向上移动,而点A向下移动,故点M会向点A靠拢,故当抛物线经过点A时, ![]() 取得最小值。将点A坐标代入抛物线,得:
取得最小值。将点A坐标代入抛物线,得: ![]()
∴![]() 。
。
(ⅱ)易求AB解析式为![]() ,将点M坐标代入直线与抛物线解析式可得:
,将点M坐标代入直线与抛物线解析式可得:
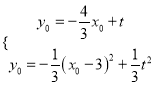 消去
消去![]() ,并化简得:
,并化简得: ![]() ,
,
由于当![]() 变成某一个值时,点A的位置唯一确定,所以上述关于
变成某一个值时,点A的位置唯一确定,所以上述关于![]() 的方程有两个相等的实数根,从而有:
的方程有两个相等的实数根,从而有:
![]() ,
, ![]()
解得: ![]() (
(![]() 舍去)
舍去)
代入AB解析式![]() ,可得:
,可得: ![]()
所以,此时点M的坐标为(![]() ,
, ![]() )
)
“点睛”此题属于二次函数综合题,涉及的知识有:二次函数的性质,待定系数法确定抛物线解析式、二次函数的最值、一元二次方程的判别式,熟练掌握待定系数法是解本题的关键,解题时要注意用分类讨论思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一列按一定顺序和规律排列的数:
第一个数是
 ;
;第二个数是
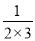 ;
;第三个数是
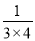 ;
;…
对任何正整数n,第n个数与第(n+1)个数的和等于
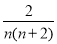 .
.(1)经过探究,我们发现:
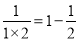 ,
,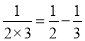 ,
, ;
;设这列数的第5个数为a,那么
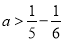 ,
,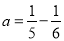 ,
,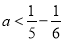 ,哪个正确?
,哪个正确?请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于
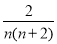 ”;
”;(3)设M表示
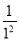 ,
,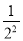 ,
,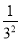 ,…,
,…,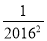 ,这2016个数的和,即
,这2016个数的和,即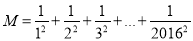 ,求证:
,求证: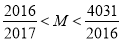 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国倡导的“一带一路”建设将促进我国与世界各国的互利合作.根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为 ( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,对角线AC=12,BD=8,交点为点O,则边AB的取值范围为( )
A.1<AB<2
B.2<AB<10
C.4<AB<10
D.4<AB<20 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+4x﹣3=0的两根为x1 , x2 , 则x1x2的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把代数式x3-2x2+x因式分解,结果是( )
A. x2(x-2)+x B. x(x2-2x)
C. x(x-1)2 D. x(x+1)(x-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】当n为自然数时,(n+1)2-(n-3)2一定能被下列哪个数整除( )
A. 5 B. 6 C. 7 D. 8
相关试题

