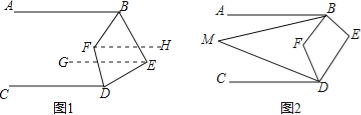
【题目】如图:已知AB∥CD,∠ABE与∠CDE两个角的角平分线相交于F.
(1)如图1,若∠E=80°,求∠BFD的度数.
(2)如图2:若∠ABM=![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
∠CDF,写出∠M和∠E之间的数量关系并证明你的结论.
(3)若∠ABM=![]() ∠ABF, ∠CDM=
∠ABF, ∠CDM=![]() ∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)
∠CDF, 设∠E=m°,直接用含有n、m°的代数式写出∠M= (不写过程)

参考答案:
【答案】(1)140°;(2)6∠M+∠E=360°.(3)![]()
【解析】试题分析:(1)首先作EG∥AB,FH∥AB,利用平行线的性质可得∠ABE+∠CDE=280°,再利用角平分线的定义得到∠ABF+∠CDF=140°,从而得到∠BFD的度数;(2)先由已知得到∠ABE=6∠ABM,∠CDE=6∠CDM,由(1)得∠ABE+∠CDE=360°﹣∠E,∠M=∠ABM+∠CDM,等量代换,即可;
(3)由(2)的方法可得到2n∠M+∠E=360°,将∠E=m°代入可得![]() .
.
解:(1)作EG∥AB,FH∥AB,
∵AB∥CD,
∴EG∥AB∥FH∥CD,
∴∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,
∴∠ABE+∠BEG+∠GED+∠CDE=360°
∵∠BED=∠BEG+∠DEG=80°,
∴∠ABE+∠CDE=280°,
∵∠ABF和∠CDF的角平分线相交于E,
∴∠ABF+∠CDF=140°,
∴∠BFD=∠BFH+∠DFH=140°;
(2)∵∠ABM=∠ABF,∠CDM=∠CDF,
∴∠ABF=3∠ABM,∠CDF=3∠CDM,
∵∠ABE与∠CDE两个角的角平分线相交于点F,
∴∠ABE=6∠ABM,∠CDE=6∠CDM,
∴6∠ABM+6∠CDM+∠E=360°,
∵∠M=∠ABM+∠CDM,
∴6∠M+∠E=360°.
(3)由(2)结论可得,
2n∠ABN+2n∠CDM+∠E=360°,∠M=∠ABM+∠CDM,
解得:![]() .
.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD是△ABC的角平分线,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )
A、DE=DF B、BD=CD
C、AE=AF D、∠ADE=∠ADF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
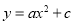 (
(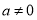 )与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.
)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一点为E,其顶点为F,对称轴与x轴的交点为H.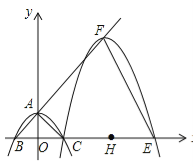
(1)求a、c的值及抛物线的解析式.(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
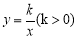 与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.
与正比例函数y=ax相交于A(1,k),B(﹣k,﹣1)两点.
(1)求反比例函数和正比例函数的解析式;
(2)将正比例函数y=ax的图象平移,得到一次函数y=ax+b的图象,与反比例函数
 的图象交于C(x1,y1),D(x2,y2),且|x1﹣x2||y1﹣y2|=5,求b的值.
的图象交于C(x1,y1),D(x2,y2),且|x1﹣x2||y1﹣y2|=5,求b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小区A与公路l的距离AC=200米,小区B与公路l的距离BD=400米,已知CD=800米,现要在公路旁建造一利民超市P,使P到A、B两小区的路程之和最短,超市应建在哪?

(1)请在图中画出点P;
(2)求CP的长度;
(3)求PA+PB的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】足球比赛的记分为:胜一场得3分,平一场得1分,负一场得0分,一队打了14场比赛,负5场,共得19分,那么这个队胜了( )
A. 6场 B. 5场 C. 4场 D. 3场
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形切去一个角后,形成的另一个多边形的内角和为1 080°,求原多边形的边数.
相关试题

