【题目】已知,如图,△ABC的三条边BC=![]() ,CA=
,CA=![]() ,AB=
,AB=![]() ,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=
,D为△ABC内一点,且∠ADB=∠BDC=∠CDA=120°,DA=![]() ,DB=
,DB=![]() ,DC=
,DC=![]() .
.
(1)若∠CDB=18°,则∠BCD= °;
(2)将△ACD绕点A顺时针方向旋转90°到![]() ,画出
,画出![]() ,若∠CAD=20°,求
,若∠CAD=20°,求![]() 度数;
度数;
(3)试画出符合下列条件的正三角形:M为正三角形内的一点,M到正三角形三个顶点的距离分别为![]() 、
、![]() 、
、![]() ,且正三角形的边长为
,且正三角形的边长为![]() +
+![]() +
+![]() ,并给予证明.
,并给予证明.

参考答案:
【答案】(1)42;
(2)画图见解析, ![]() 度数是70°;
度数是70°;
(3)画图见解析,证明见解析
【解析】(本小题满分14分)
解:(1)42;……………………………………………………………………1分
(2)画图如下(如图5).………………………………………………………3分
∵∠DA![]() =90°,∠CAD=20°,
=90°,∠CAD=20°,
∴∠CA![]() =∠DA
=∠DA![]() -∠CAD=90°-20°=70°;…………5分
-∠CAD=90°-20°=70°;…………5分
![]()
(3)画图如下:将△BDC绕点B按逆时针方向旋转60°…………………2分
到△BEF的位置(如图6).
连结DE,CF,这样可知△BDE和△BCF均为等边三角形,
从而DE=![]() ,CF=
,CF=![]() .
.
∵∠ADB=120°,∠BDE=60°,即∠ADE=180°,
则A、D、E三点共线(即该三点在同一条直线上).……………………………3分
同理,∵∠BEF=∠BDC=120°,∠BED=60°,
即∠DEF=180°,则D、E、F三点共线,
∴A、D、E、F四点均在一条直线上.…………………………………………4分
∵EF=DC=![]() ,∴线段AF=
,∴线段AF=![]() +
+![]() +
+![]() .
.
以线段AF为边在点B一侧作等边△AFG(图6),……………………………5分
则△AFG即为符合条件的等边三角形,其中的点B即为点M.…………………6分
正三角形的边长为![]() +
+![]() +
+![]() 已证,BA=
已证,BA=![]() ,BF=BC=
,BF=BC=![]() ,
,
下面再证BG=![]() .
.
∵∠CFB=∠AFG=60°,
即∠1+∠EFB=∠2+∠EFB=60°,∴∠1=∠2.
在△AFC和△GFB中,∵FA=FG,∠1=∠2,FC=FB,
∴△AFC≌△GFB(SAS),
∴AC=GB,即BG=CA=![]() .
.
从而点B(M)到等边△AFG三个顶点的距离分别为![]() 、
、![]() 、
、![]() ,
,
且其边长为![]() +
+![]() +
+![]() .………………………………………………………………8分
.………………………………………………………………8分
[注:把△ADB绕点A按逆时针方向旋转60°,
把△CDA绕点C按逆时针方向旋转60°,
把△ADC绕点A按顺时针方向旋转60°,
把△BCD绕点C按顺时针方向旋转60°等
均可证得,方法类似]
-
科目: 来源: 题型:
查看答案和解析>>【题目】在列分式方程解应用题时:
(1)主要步骤有:①审清题意;②设未知数;③根据题意找关系,列出分式方程;④解方程,并;⑤写出答案.
(2)请你联系实际设计一道关于分式方程 =
=  的应用题,要求表述完整,条件充分,并写出解答过程.
的应用题,要求表述完整,条件充分,并写出解答过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是S小刘2=0.6,S小李2=1.4,那么两人中射击成绩比较稳定的是______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,属于中心对称图形的是( )
A.锐角三角形B.直角三角形C.菱形D.对角互补的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个正数a,b,可按规则c=ab+a+b扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作。
(1)若a=1,b=3,按上述规则操作3次,扩充所得的数是__________;
(2)若p>q>0,经过3次操作后扩充所得的数为
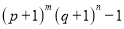 (m,n为正整数),则m,n的值分别为__________.
(m,n为正整数),则m,n的值分别为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】角是一个轴对称图形,角的对称轴是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中最适合使用普查方式收集数据的是( )
A.为制作校服,了解某班同学的身高情况
B.了解全市初三学生的视力情况
C.了解一种节能灯的使用寿命
D.了解我省农民的年人均收入情况
相关试题

