【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( ) 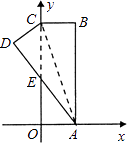
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:如图,过D作DF⊥AF于F, 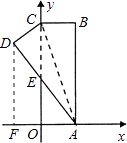
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2 ,
∴(3﹣x)2=x2+12 ,
∴x= ![]() ,
,
又DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
而AD=AB=3,
∴AE=CE=3﹣ ![]() =
= ![]() ,
,
∴ ![]() ,
,
即 ![]() ,
,
∴DF= ![]() ,AF=
,AF= ![]() ,
,
∴OF= ![]() ﹣1=
﹣1= ![]() ,
,
∴D的坐标为(﹣ ![]() ,
, ![]() ).
).
故选A.
如图,过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=1,设OE=x,那么CE=3﹣x,DE=x,利用勾股定理即可求出OE的长度,而利用已知条件可以证明△AEO∽△ADF,而AD=AB=3,接着利用相似三角形的性质即可求出DF、AF的长度,也就求出了D的坐标.
-
科目: 来源: 题型:
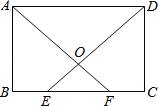
查看答案和解析>>【题目】(10分)如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.
求证:(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如果-axym是关于x,y的单项式,且系数是4,次数是5,那么a与m的值分别是________;
(2)如果-(a-2)xym是关于x,y的五次单项式,那么a与m应满足的条件是____________;
(3)如果单项式2x3y4与-
 x2zn的次数相同,那么n=________.
x2zn的次数相同,那么n=________. -
科目: 来源: 题型:
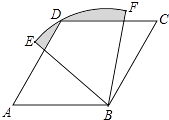
查看答案和解析>>【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )
A.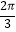 ﹣
﹣ 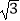 ??
??
B.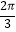 ﹣
﹣ 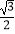 ??
??
C.π﹣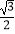 ??
??
D.π﹣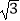
-
科目: 来源: 题型:
查看答案和解析>>【题目】在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.

(1)求证:四边形DEGF是平行四边形;
(2)当点G是BC的中点时,求证:四边形DEGF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个锐角的和等于90°,那么我们就称这两个角互为余角.类似可以定义:如果两个角的差的绝对值等于90°,那么我们就可以称这两个角互为垂角.例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角).
(1)如图,O为直线AB上一点,OC⊥AB于点O,OE⊥OD于点O ,请写出图中所有互为垂角的角:_______________________________________________________;
(2)如果一个角的垂角等于这个角的补角的
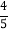 ,求这个角的度数.
,求这个角的度数.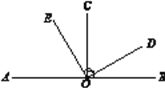
相关试题

