【题目】某移动公司开设了两种通信业务:“全球通”要缴月租费50元。另外每分钟通话费0.4元;“神州行”不缴月租费,但每分钟通话费0.6元.若一个月通话![]() ,两种收费方式的费用分别为
,两种收费方式的费用分别为![]() 和
和![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式?
的函数解析式?
(2)一个月内通话多少分钟,两种收费方式的费用是相同的?
(3)=若![]() ,选择哪种收费方式更合适?
,选择哪种收费方式更合适?
参考答案:
【答案】(1)y1 =50+0.4x,y2 =0.6x;(2)250分钟;(3)选择“全球通”合算.
【解析】试题分析:(1)根据:全球通”使用者先缴50元月基础费,然后每通话1分钟,再付电话费0.4元;“神州行”不缴月基础费,每通话1分钟,付话费0.6元,可将通讯费用和通话时间的函数关系式求出;(2)令y1=y2,得出关于x的方程,解方程即可求得;(3)把x=300代入解析式求出y的值比较即可.
试题解析:(1)根据题意得:y1=50+0.4x;y2=0.6x;
(2)当y1=y2,则50+0.4x=0.6x,
解得x=250.
∴通话250分钟两种费用相同;
(3)当x=300时,y1=50+0.4x=50+0.4×300=170,
y2=0.6x=0.6×300=180,
∴y1<y2,
∴选择“全球通”比较合算。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.
(1)求证:OE=OF.
(2)在点E、F的运动过程中,连结AF.设线段AE、OE、OF、AF所形成的图形面积为S.
探究:①S的大小是否会随着运动时间为t的变化而变化?若会变化,试求出S与t的函数关系式;若不会变化,请说明理由.
②连结EF,当运动时间为t为何值时,△OEF的面积恰好等于的
 S.
S. 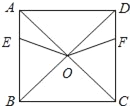
-
科目: 来源: 题型:
查看答案和解析>>【题目】减去-x2+6x-5等于4x2+3x-5的多项式是________________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2﹣2x=0的解是( )
A. x=2 B. x=0 C. x1=0,x2=﹣2 D. x1=0,x2=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b﹣1)2=0.点A与点B之间的距离表示为AB(以下类同).
(1)求AB的长;
(2)点C在数轴上对应的数为x,且x是方程2x﹣2=
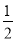 x+2的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
x+2的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;(3)在(1)、(2)的条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和C分别以每秒4个单位长度和9个单位长度的速度向右运动,经过t秒后,请问:AB﹣BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
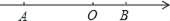
-
科目: 来源: 题型:
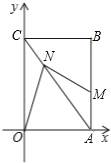
查看答案和解析>>【题目】已知:矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒.
(1)当点N运动1秒时,求点N的坐标;(提示:过N作x轴y轴垂线,垂足分别为D,ECN:CA=CE:CO=NE:OA)
(2)试求出多边形OAMN的面积S与t的函数关系式;
(3)t为何值时,以△OAN的一边所在直线为对称轴翻折△OAN,翻折前后的两个三角形所组成的四边形为菱形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两圆半径分别为6cm和5cm,圆心距为1cm,则这两个圆( )
A. 外切 B. 内切 C. 相交 D. 相离
相关试题

