搜索
【题目】两圆半径分别为6cm和5cm，圆心距为1cm，则这两个圆（ ）
A. 外切 B. 内切 C. 相交 D. 相离
参考答案：
【答案】B
【解析】
根据圆心距与半径的关系即可判断．
∵圆心距d=1，R=6，r=5，
∴d=R﹣r，
∴两圆内切．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某移动公司开设了两种通信业务：“全球通”要缴月租费50元。另外每分钟通话费0.4元；“神州行”不缴月租费，但每分钟通话费0.6元.若一个月通话
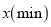，两种收费方式的费用分别为
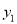和
元.（1）求
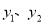与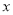
的函数解析式？（2）一个月内通话多少分钟，两种收费方式的费用是相同的？
（3）=若
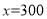，选择哪种收费方式更合适？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，若点A在数轴上对应的数为a，点B在数轴上对应的数为b，且a，b满足|a+2|+（b﹣1）2=0．点A与点B之间的距离表示为AB（以下类同）．
（1）求AB的长；
（2）点C在数轴上对应的数为x，且x是方程2x﹣2=
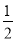x+2的解，在数轴上是否存在点P，使得PA+PB=PC？若存在，求出点P对应的数；若不存在，说明理由；（3）在（1）、（2）的条件下，点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和C分别以每秒4个单位长度和9个单位长度的速度向右运动，经过t秒后，请问：AB﹣BC的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其常数值．
-
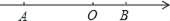
科目： 来源： 题型：
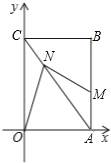
查看答案和解析>>【题目】已知：矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴上，且OA=3cm，OC=4cm，点M从点A出发沿AB向终点B运动，点N从点C出发沿CA向终点A运动，点M、N同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．
（1）当点N运动1秒时，求点N的坐标；(提示:过N作x轴y轴垂线，垂足分别为D,ECN:CA=CE:CO=NE:OA)
（2）试求出多边形OAMN的面积S与t的函数关系式；
（3）t为何值时，以△OAN的一边所在直线为对称轴翻折△OAN，翻折前后的两个三角形所组成的四边形为菱形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是（ ）
A.3，4，5B.4，5，6C.34,54，1D.9，12，16
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数y＝kx＋b的图像与反比例函数
的图像交于A、B两点，且点A的横坐标和点B的纵坐标都是- 2，一次函数图像与x轴交于点M．(1)在如图的直角坐标系中画出这两个函数的图像．
(2) 求一次函数的解析式．
(3)方程
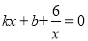的解为：_______________；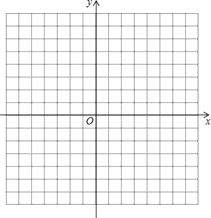
-
科目： 来源： 题型：
查看答案和解析>>【题目】若△ABC∽△DEF ， 若∠A=50°，∠B=60°，则∠F的度数是（ ）
A. 50° B. 60° C. 70° D. 80°
相关试题
