【题目】如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n,且m、n满足m= ![]() +
+ ![]() +2,试求BE的长.
+2,试求BE的长. 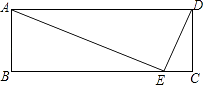
参考答案:
【答案】解:∵m、n满足m= ![]() +
+ ![]() +2,
+2,
∴ ![]() ,
,
∴n=8,
∴m=2,
∵DE=m+n,
∴DE=10,
∵AE⊥DE,∠DAE=30°,
∴AD=2DE=20,∠ADE=60°,
∵四边形ABCD是矩形,
∴∠ADC=90°,BC=AD=20,
∴∠CDE=30°,
∴CE= ![]() DE=5,
DE=5,
∴BE=BC﹣CE=20﹣5=15.
【解析】根据二次根式的意义求出m、n,得出DE,再由含30°角的直角三角形的性质得出AD,由矩形的性质得出∠ADC=90°,BC=AD=20,得出∠CDE=30°,求出CE,即可得出BE的长.
【考点精析】本题主要考查了二次根式有意义的条件和矩形的性质的相关知识点,需要掌握被开方数必须为非负数,如果分母中有根式,那么被开方数必须是正数,因为零不能做分母;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的各组线段能组成一个三角形的是( ).
A. 4cm,6cm,11cm B. 4cm,5cm,1cm
C. 3cm,4cm,5cm D. 2cm,3cm,6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点A(1,﹣3),B(m,3)在同一反比例函数的图象上,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 ,
,  ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查,下面是根据收集的数据绘制的两幅不完整的统计图.
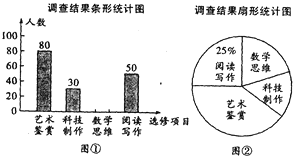
根据图中提供的信息,解答下列问题:
(1)此次共调查了 名学生,扇形统计图中,“艺术鉴赏”所对应的圆心角的度数是 度;
(2)请把这个条形统计图补充完整;
(3)现该校700名学生报名参加这四个选修项目,请你估计有多少名学生参加了“数学思维”项目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC三条边长为a,b,c,化简:|a﹣b﹣c|﹣|a+c﹣b|= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为
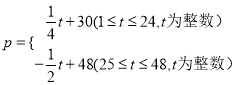 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
相关试题

