Question

【题目】如图，抛物线y=ax2+bx﹣2与x轴交于A、B两点，与y轴交于C点，已知A（3，0），且M（1，﹣ ）是抛物线上另一点．

（1）求a、b的值；
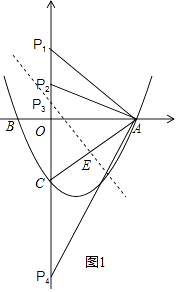
（2）连结AC，设点P是y轴上任一点，若以P、A、C三点为顶点的三角形是等腰三角形，求P点的坐标；
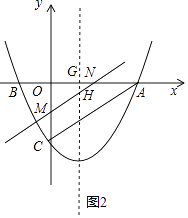
（3）若点N是x轴正半轴上且在抛物线内的一动点（不与O、A重合），过点N作NH∥AC交抛物线的对称轴于H点．设ON=t，△ONH的面积为S，求S与t之间的函数关系式．

Answer 1

【答案】
（1）

解：把A（3，0），且M（1，﹣ ）代入y=ax2+bx﹣2得 ，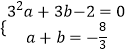

解得：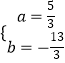

（2）

解：在y=ax2+bx﹣2中，当x=0时．y=﹣2，

∴C（0，﹣2），

∴OC=2，

如图，设P（0，m），则PC=m+2，OA=3，AC= = ，

①当PA=CA时，则OP1=OC=2，

∴P1（0，2）；

②当PC=CA= 时，即m+2= ，∴m= ﹣2，

∴P2（0， ﹣2）；

③当PC=PA时，点P在AC的垂直平分线上，

则△AOC∽△P3EC，

∴ = ，

∴P3C= ，

∴m= ，

∴P3（0， ），

④当PC=CA= 时，m=﹣2﹣ ，

∴P4（0，﹣2﹣ ），

综上所述，P点的坐标1（0，2）或（0， ﹣2）或（0， ）或（0，﹣2﹣ ）

（3）

解：过H作HG⊥OA于G，设HN交Y轴于M，

∵NH∥AC，

∴ ，

∴ ，

∴OM= ，

∵抛物线的对称轴为直线x= = ，

∴OG= ，

∴GN=t﹣ ，

∵GH∥OC，

∴△NGH∽△NOM，

∴ ，

即 = ，

∴HG= t﹣ ，

∴S= ONGH= t（ t﹣ ）= t2﹣ t（0＜t＜3）．

【解析】（1）根据题意列方程组即可得到结论；（2）在y=ax2+bx﹣2中，当x=0时．y=﹣2，得到OC=2，如图，设P（0，m），则PC=m+2，OA=3，根据勾股定理得到AC= = ，①当PA=CA时，则OP1=OC=2，②当PC=CA= 时，③当PC=PA时，点P在AC的垂直平分线上，根据相似三角形的性质得到P3（0， ），④当PC=CA= 时，于是得到结论；（3）过H作HG⊥OA于G，设HN交Y轴于M，根据平行线分线段成比例定理得到OM= ，求得抛物线的对称轴为直线x= = ，得到OG= ，求得GN=t﹣ ，根据相似三角形的性质得到HG= t﹣ ，于是得到结论．
【考点精析】根据题目的已知条件，利用勾股定理的概念和平行线分线段成比例的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；三条平行线截两条直线，所得的对应线段成比例．