【题目】恒昌路是一条东西走向的马路,有市场、医院、车站、学校四家公共场所。已知市场在医院东200米,车站在市场东150米,医院在学校东450米。若将马路近似的看成一条直线,以医院为原点,向东方向为正方向,用1个单位长度表示100米,
(1)在数轴上表示出四家公共场所的位置;
![]()
(2)列式计算学校与车站之间的距离.
参考答案:
【答案】(1)见详解;(2)学校与车站之间的距离为800米.
【解析】
(1)规定向东为正,注意单位长度是以100米为1个单位,画出图形即可;
(2)根据数轴上两点之间的距离是表示这两点的数的差的绝对值,计算即可得到答案;
解:(1)以医院为原点,则四家公共场所的位置如图所示:
 ;
;
(2)由(1)可知,学校为![]() ,车站为
,车站为![]() ,
,
∴学校到车站的距离为:![]() 米;
米;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:a是最大的负整数,b是最小的正整数,且c=a+b,请回答下列问题:

(1)请直接写出a,b,c的值:a= ;b= ;c= ;
(2)a,b,c在数轴上所对应的点分别为A,B,C,请在如图的数轴上表示出A,B,C三点;
(3)在(2)的情况下.点A,B,C开始在数轴上运动,若点A,点C以每秒1个单位的速度向左运动,同时,点B以每秒5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求出AB﹣BC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将函数y=
 (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
A.
 B.
B. 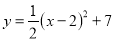
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线经过点D和杯子上底面中心E,则点E到洗手盆内侧的距离EH为_________cm.

(第16题图)
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站
A
B
C
D
E
x(千米)
8
9
10
11.5
13
y1(分钟)
18
20
22
25
28
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=
 x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】【探索发现】
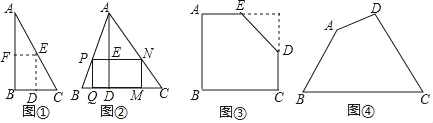
如图①,是一张直角三角形纸片,∠B=90°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=
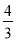 ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
相关试题

