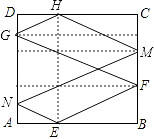
【题目】如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P与正方形的边碰撞的次数为 , 小球P所经过的路程为 . 
参考答案:
【答案】6;6 ![]()
【解析】解:根据已知中的点E,F的位置,可知入射角的正切值为 ![]() ,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得, 第二次碰撞点为G,在DA上,且DG=
,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得, 第二次碰撞点为G,在DA上,且DG= ![]() DA,
DA,
第三次碰撞点为H,在DC上,且DH= ![]() DC,
DC,
第四次碰撞点为M,在CB上,且CM= ![]() BC,
BC,
第五次碰撞点为N,在DA上,且AN= ![]() AD,
AD,
第六次回到E点,AE= ![]() AB.
AB.
由勾股定理可以得出EF= ![]() ,FG=
,FG= ![]()
![]() ,GH=
,GH= ![]()
![]() ,HM=
,HM= ![]() ,MN=
,MN= ![]()
![]() ,NE=
,NE= ![]()
![]() ,
,
故小球经过的路程为: ![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]() +
+ ![]()
![]() +
+ ![]()
![]() =6
=6 ![]() ,
,
所以答案是:6;6 ![]() .
.
【考点精析】通过灵活运用正方形的性质和轴对称的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①要了解一批灯泡的使用寿命,应采用普查的方式;
②若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖;
③甲、乙两组数据的样本容量与平均数分别相同,若方差 =0.1,
=0.1,  =0.2,则甲组数据比乙组数据稳定;
=0.2,则甲组数据比乙组数据稳定;
④“掷一枚硬币,正面朝上”是必然事件.
正确说法的序号是( )
A.①
B.②
C.③
D.④ -
科目: 来源: 题型:
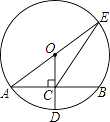
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2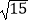
B.8
C.2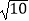
D.2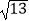
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,已知线段AO=2,⊙A的半径为1,将⊙A绕点O按逆时针方向旋转60°得到的像为⊙B,则⊙A与⊙B的位置关系为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
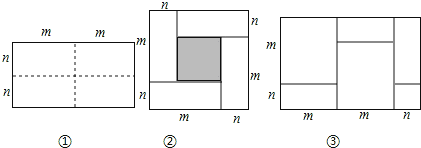
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:|﹣4|﹣ +(﹣2)0;
+(﹣2)0;
(2)化简:a(b+1)﹣ab﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DE,∠ABC=65°,∠CDE=138°,则∠C的值为( )

A.21°
B.23°
C.25°
D.30°
相关试题

