【题目】问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c=①______,
因为c=13,所以a+b=②______,
所以(a+b)2=③______,所以a2+ b2+④_____=289.
因为a2+b2=c2,所以c2+2ab=289,
所以⑤______+2ab=289,所以ab=⑥______(第1步),
所以△ABC的面积=![]() ab=
ab=![]() ×⑦______=⑧______(第2步).
×⑦______=⑧______(第2步).
合作探究:(1)对解法展示进行填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是______(填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
参考答案:
【答案】(1)①30,②17,③172(或289),④2ab,⑤132(或169),⑥ab=60,⑦60,⑧30;(2)①;(3)这个直角三角形的周长是24.
【解析】
(1)根据三角形的周长定义,勾股定理,三角形的面积公式即可求解;
(2)根据(1)的解答过程得到由第1步到第2步体现出来的数学思想是整体思想;
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数).利用勾股定理和三角形的面积公式求得两直角边是6和8.然后由三角形的周长公式求得该直角三角形的周长.
(1) 设Rt△ABC的两直角边长分别为a,b,则a+b+c=①___30___,
因为c=13,所以a+b=②___17___,
所以(a+b)2=③___172(或289)___,所以a2+ b2+④_2ab ___=289.
因为a2+b2=c2,所以c2+2ab=289,
所以⑤___132(或169)___+2ab=289,所以ab=⑥____60__(第1步),
所以△ABC的面积=![]() ab=
ab=![]() ×⑦___60___=⑧__30____(第2步).
×⑦___60___=⑧__30____(第2步).
(2) 根据(1)的解答过程得到由第1步到第2步体现出来的数学思想是整体思想,故选①;
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数),则依题意得:

解得![]()
所以这个直角三角形的周长是:6+8+10=24.
∴这个直角三角形的周长是24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:

(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,

(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+(k+3)x+
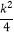 =0有两个不相等的实数根.
=0有两个不相等的实数根.(1)求k的取值范围;
(2)若方程两根为x1,x2,那么是否存在实数k,使得等式
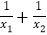 =﹣1成立?若存在,求出k的值;若不存在,请说明理由.
=﹣1成立?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
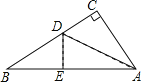
A. 3cmB. 4cmC. 5cmD. 6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,直线y=
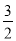 x+b与直线y=
x+b与直线y= x交于点A(m,1).与y轴交于点B
x交于点A(m,1).与y轴交于点B(1)求m的值和点B的坐标;
(2)若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.
-
科目: 来源: 题型:
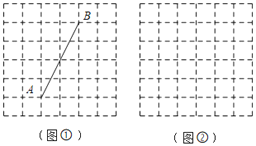
查看答案和解析>>【题目】如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点.
(1)在图①中,线段AB的长度为 ;若在图中画出以C为直角顶点的Rt△ABC,使点C在格点上,请在图中画出所有点C;
(2)在图②中,以格点为顶点,请先用无刻度的直尺画正方形ABCD,使它的面积为13;再画一条直线PQ(不与正方形对角线重合),使PQ恰好将正方形ABCD的面积二等分(保留作图痕迹).
相关试题

